-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478311 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 533027 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496525 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 709229 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2127594 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Questioner » Dom Mai 16, 2010 18:15
por Questioner » Dom Mai 16, 2010 18:15
Olá,
Estou com uma dúvida na seguinte questão:
Se

para
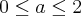
.
Encontre a função

O gabarito seria:
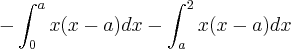
Que seria igual a
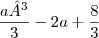
Tudo bem, resolver a integral é fácil. Mas, teoricamente, por que separar as integrais de 0 a A e de A a 2? E por que elas devem ficar negativas?
Valeu!
-
Questioner
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Abr 20, 2010 22:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cahu » Qua Abr 20, 2011 23:11
por Cahu » Qua Abr 20, 2011 23:11
Se f(a) = \int_{0}^{2}|x(x-a)|dx para 0\leq a \leq 2.
como o 0<a<2 e 0<x<2 entao para x(x-a) com x<a temos que o resultado dessa integral é negativa, por isso o sinal de menos e a divisão para 2 integrais, a segunda parte pode ser feita normalmente pois o valor é positivo e não precisa do sinal de menos.
-\int_{0}^{a}x(x-a)dx + \int_{a}^{2} x(x-a)dx
-
Cahu
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Abr 20, 2011 23:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrônica
- Andamento: cursando
 por LuizAquino » Qui Abr 21, 2011 09:38
por LuizAquino » Qui Abr 21, 2011 09:38
Questioner escreveu:Mas, teoricamente, por que separar as integrais de 0 a A e de A a 2? E por que elas devem ficar negativas?
Do ponto de vista teórico, é necessário apenas lembrar da definição de módulo de um número real
x:
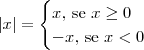
Desse modo, aplicando a definição para |x(x-a)| (lembrando que
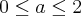
e
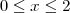
neste exercício):
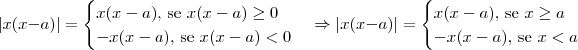
Portanto, temos que:
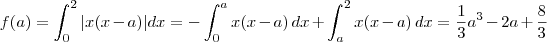
.
Note que apenas na primeira integral deve aparecer o sinal negativo antes dela.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral com módulo.
por adecris » Sex Nov 11, 2011 13:01
- 1 Respostas
- 4191 Exibições
- Última mensagem por LuizAquino

Sex Nov 11, 2011 17:12
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Módulo
por iagoyotsui » Ter Set 24, 2013 19:18
- 1 Respostas
- 1855 Exibições
- Última mensagem por Russman

Ter Set 24, 2013 21:43
Cálculo: Limites, Derivadas e Integrais
-
- [integral definida com modulo]
por Giu » Qua Fev 08, 2012 16:08
- 1 Respostas
- 7161 Exibições
- Última mensagem por LuizAquino

Qua Fev 08, 2012 16:53
Cálculo: Limites, Derivadas e Integrais
-
- [integral envolvendo módulo]
por Fabio Wanderley » Sex Dez 14, 2012 11:14
- 3 Respostas
- 2277 Exibições
- Última mensagem por young_jedi

Sex Dez 14, 2012 16:04
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] com modulo nos limites de integração
por flavia_carolinee » Ter Jun 04, 2013 18:32
- 0 Respostas
- 2389 Exibições
- Última mensagem por flavia_carolinee

Ter Jun 04, 2013 18:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 para
para 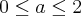 .
.
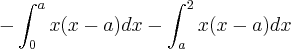
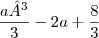



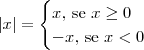
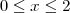 neste exercício):
neste exercício):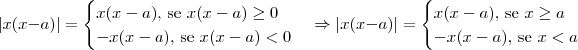
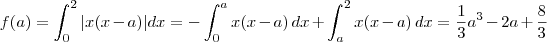 .
.