 por felipe_ad » Sáb Abr 24, 2010 15:00
por felipe_ad » Sáb Abr 24, 2010 15:00
Olá
Estou com duas duvidas sobre limites no infinito.
A primeira é sobre o estudo do sinal do numero proximo de zero no denominador. Ex: lim(2x5-3x²+2)/-x²+7 quando x->+infinito
A outra é sobre como identificar uma indeterminaçao do tipo "infinito-infinito", por exemplo, no seguinte limite: lim(3x5-4x³+1) quando x->+infinito
Tenho prova segunda, me ajudem rsrs
Agradeço desde já
-
felipe_ad
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 03, 2010 12:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por MarceloFantini » Sáb Abr 24, 2010 18:34
por MarceloFantini » Sáb Abr 24, 2010 18:34
Felipe, esclareça:

;
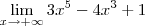
.
Se forem estes os casos, no segundo acredito que não exista determinação, pois

cresce muito mais que

, então o limite é infinito mesmo. Indeterminação é quando se tem

. No primeiro, eu faria assim:
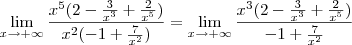
. Quando x está tendendo ao infinito,

todos tendem a 0, sobrando
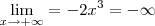
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por felipe_ad » Sáb Abr 24, 2010 19:29
por felipe_ad » Sáb Abr 24, 2010 19:29
No primeiro caso, entendi como vc fez. Mas é que no livro que tenho, ensina diferente: divide todos os termos pelo termo de maior grau, no caso

, ai o denominador ficaria

, como
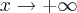
, o denominador seria 0, daí ele (o livro) fala que se for

, no caso algum número que se aproxime de zero pela esquerda, o limite seria

. É ai que queria saber como saber o sinal desse número aproximado de zero.
O segundo caso, tá tranquilo já.
Obrigado.
-
felipe_ad
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Abr 03, 2010 12:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por MarceloFantini » Dom Abr 25, 2010 02:27
por MarceloFantini » Dom Abr 25, 2010 02:27
Eu aprendi a colocar as maiores potências em evidência e trabalhar daí pra frente. Qual método você achou mais fácil de trabalhar? Escolha aquele que você entenda o conceito e sinta-se confortável em trabalhar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3520 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4771 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Dúvida em questão de Limites no infinito
 por Jacques » Ter Jul 12, 2016 21:42
por Jacques » Ter Jul 12, 2016 21:42
- 4 Respostas
- 7540 Exibições
- Última mensagem por vitor_jo

Qua Jul 13, 2016 16:51
Cálculo: Limites, Derivadas e Integrais
-
- Limites no infinito
por jr_freitas » Sex Out 07, 2011 16:55
- 10 Respostas
- 10047 Exibições
- Última mensagem por Claudin

Sáb Out 08, 2011 20:03
Cálculo: Limites, Derivadas e Integrais
-
- Limites no infinito
por Rosi7 » Sáb Mai 02, 2015 19:13
- 3 Respostas
- 2875 Exibições
- Última mensagem por DanielFerreira

Dom Mai 03, 2015 15:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ;
; 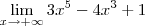 .
. cresce muito mais que
cresce muito mais que  , então o limite é infinito mesmo. Indeterminação é quando se tem
, então o limite é infinito mesmo. Indeterminação é quando se tem  . No primeiro, eu faria assim:
. No primeiro, eu faria assim: 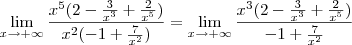 . Quando x está tendendo ao infinito,
. Quando x está tendendo ao infinito,  todos tendem a 0, sobrando
todos tendem a 0, sobrando 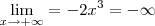 .
.

 , ai o denominador ficaria
, ai o denominador ficaria  , como
, como 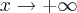 , o denominador seria 0, daí ele (o livro) fala que se for
, o denominador seria 0, daí ele (o livro) fala que se for  , no caso algum número que se aproxime de zero pela esquerda, o limite seria
, no caso algum número que se aproxime de zero pela esquerda, o limite seria  . É ai que queria saber como saber o sinal desse número aproximado de zero.
. É ai que queria saber como saber o sinal desse número aproximado de zero.