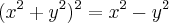por gabrielb44 » Sáb Nov 18, 2017 20:35
por gabrielb44 » Sáb Nov 18, 2017 20:35
Considere a lemniscata de equação:
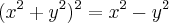
Determine os dois pontos da lemniscata em que as tangentes são verticais.
Eu adaptei o problema, o original pedia também os pontos em que a reta tangente é horizontal, mas esses pontos eu consegui achar.
Já procurei na internet mas não achei nenhum lugar que explica como achar os pontos em que a reta tangente é vertical.
Se alguém poder pelo menos me explicar como descobrir os pontos em que a reta é vertical me ajudaria bastante.
Grato.
Gabriel Leite
Estudante de Ciência da Computação
-
gabrielb44
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Nov 18, 2017 20:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computção
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [reta vertical e horizontal]não consigo achar o valor.
por marcosmuscul » Qui Abr 04, 2013 17:34
- 1 Respostas
- 2000 Exibições
- Última mensagem por Russman

Qui Abr 04, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada Implícita]Encontrar os pontos onde tg é horizontal
 por narcpereira » Sáb Mai 16, 2015 10:20
por narcpereira » Sáb Mai 16, 2015 10:20
- 1 Respostas
- 2457 Exibições
- Última mensagem por nakagumahissao

Ter Out 06, 2015 13:58
Cálculo: Limites, Derivadas e Integrais
-
- [Equação da Reta] Reta que passa por pontos do plano.
por acorreia » Qua Mai 02, 2012 17:31
- 1 Respostas
- 2465 Exibições
- Última mensagem por Russman

Qua Mai 02, 2012 21:25
Geometria Analítica
-
- [ESTUDO DA RETA] Ponto da reta, com os pontos A e B sendo eq
 por rochadapesada » Dom Dez 15, 2013 16:31
por rochadapesada » Dom Dez 15, 2013 16:31
- 8 Respostas
- 5367 Exibições
- Última mensagem por rochadapesada

Dom Dez 15, 2013 21:14
Geometria Analítica
-
- [DERIVADA] Reta tangente e Reta perpendicular
por antonelli2006 » Ter Nov 22, 2011 11:21
- 1 Respostas
- 8666 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.