Uma escada de 10m de comprimento está apoiada em uma parede vertical. Se a base da escada desliza afastando-se da parede a uma taxa de 0,5m/s, determine:
a) quão rápido o topo da escada está escorregando para baixo quando a base da escada está a 6m da parede?
b) O tempo necessário para que o centro de gravidade da escada desça 3m?
Bom, estava tentando resolver esse exercício. Na letra a) eu cheguei na seguinte resposta: dy/dt = -0,375 m/s
Mas na letra b) eu não sei como proceder... Se alguém puder confirmar se a resposta que encontrei na letra a) está correta e ainda me dizer como posso resolver a letra b) eu agradeceria muito
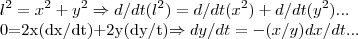
![{l}^{2}={x}^{2}+{y}^{2}\Rightarrow y=\sqrt[]{({10}^{2}-{6}^{2}}=\sqrt[]{64}=8...](/latexrender/pictures/fdd0e774a1a6675a47869647be6ff70d.png "{l}^{2}={x}^{2}+{y}^{2}\Rightarrow y=\sqrt[]{({10}^{2}-{6}^{2}}=\sqrt[]{64}=8...")
,logo: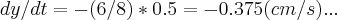
![{v}_{c}=\sqrt[]{{dx/dt}^{2}+{dy/dt}^{2}}=\sqrt[]{{0.5}^{2}+{(-0.375}^{2}}=0.625 cm/s...](/latexrender/pictures/c2f40b86794c80339d6be6771066695d.png "{v}_{c}=\sqrt[]{{dx/dt}^{2}+{dy/dt}^{2}}=\sqrt[]{{0.5}^{2}+{(-0.375}^{2}}=0.625 cm/s...")
...
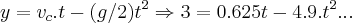
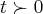![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)