 por Jadiel Carlos » Qua Nov 23, 2016 01:16
por Jadiel Carlos » Qua Nov 23, 2016 01:16
Olá pessoal... estava estudando exemplos de espaços topológicos, em particular os espaços métricos. Fiquei com a seguinte curiosidade: Um exemplo de espaço topológico que não seja espaço espaço métrico. Se alguém souber, já agradeço.
-
Jadiel Carlos
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Nov 07, 2016 00:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: cursando
 por adauto martins » Qua Nov 23, 2016 19:12
por adauto martins » Qua Nov 23, 2016 19:12
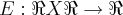
,tal que

...

é topologico,mas nao metrico,pois:
dados
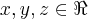
,nem sempre podemos ter:

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Jadiel Carlos » Qui Nov 24, 2016 01:10
por Jadiel Carlos » Qui Nov 24, 2016 01:10
Olá Adauto Martins, acabei de observar a resposta e entendi que vc quis dizer que o

é espaço topológico mas não é espaço métrico, pois aquela função d(x, y) não caracteriza uma métrica. Agora a minha duvida tá em saber se essa mesma função d( x, y) é que fornece os abertos da topologia de

?
-
Jadiel Carlos
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Nov 07, 2016 00:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: cursando
 por adauto martins » Qui Nov 24, 2016 12:34
por adauto martins » Qui Nov 24, 2016 12:34
meu caro colega,
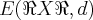
é espaço metrico dependendo da metrica

...
a metrica dada por mim,nao cumpre a condiçao da desiqualdade treiangular...
existem muitas metricas em
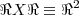
,tais como:
![d(x,y)=\left|x-y \right|...d={x}^{2}+{y}^{2}...d=\left|{x}^{2}-{y}^{2} \right|...d=\sqrt[]{{x}^{2}+{y}^{2}}(mostre-as!)..etc... d(x,y)=\left|x-y \right|...d={x}^{2}+{y}^{2}...d=\left|{x}^{2}-{y}^{2} \right|...d=\sqrt[]{{x}^{2}+{y}^{2}}(mostre-as!)..etc...](/latexrender/pictures/25f8be7cac72f2847dc43ade7645d25b.png)
...
uma metrica pode ser um caminho,uma curva,uma reta etc...desde q. satisfaça as condiçoes de metrica,tanto em abertos como fechados...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Jadiel Carlos » Qui Nov 24, 2016 13:23
por Jadiel Carlos » Qui Nov 24, 2016 13:23
Agora entendi amigo. Essa curiosidade surgiu quando eu vi a seguinte afirmação: Todo espaço métrico é espaço topológico. Valeu... Entendi agora.
-
Jadiel Carlos
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Nov 07, 2016 00:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



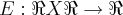 ,tal que
,tal que  ...
... é topologico,mas nao metrico,pois:
é topologico,mas nao metrico,pois: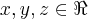 ,nem sempre podemos ter:
,nem sempre podemos ter:

 é espaço topológico mas não é espaço métrico, pois aquela função d(x, y) não caracteriza uma métrica. Agora a minha duvida tá em saber se essa mesma função d( x, y) é que fornece os abertos da topologia de
é espaço topológico mas não é espaço métrico, pois aquela função d(x, y) não caracteriza uma métrica. Agora a minha duvida tá em saber se essa mesma função d( x, y) é que fornece os abertos da topologia de  ?
?
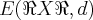 é espaço metrico dependendo da metrica
é espaço metrico dependendo da metrica  ...
...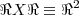 ,tais como:
,tais como:![d(x,y)=\left|x-y \right|...d={x}^{2}+{y}^{2}...d=\left|{x}^{2}-{y}^{2} \right|...d=\sqrt[]{{x}^{2}+{y}^{2}}(mostre-as!)..etc... d(x,y)=\left|x-y \right|...d={x}^{2}+{y}^{2}...d=\left|{x}^{2}-{y}^{2} \right|...d=\sqrt[]{{x}^{2}+{y}^{2}}(mostre-as!)..etc...](/latexrender/pictures/25f8be7cac72f2847dc43ade7645d25b.png) ...
...



 , avisa que eu resolvo.
, avisa que eu resolvo.

