Olá lucas92. Para encontrar o limite abaixo, eu usei a
regra de L'Hopital (assunto estudado em derivadas, caso haja duvidas sobre o método é só consultar um livro de cálculo). Comecemos:
Podemos observar que:
![\lim_{x\rightarrow 1} [2(x-1)]^2 = 0 \lim_{x\rightarrow 1} [2(x-1)]^2 = 0](/latexrender/pictures/c19f117c05ecb459a3a05058f61d382a.png)
;
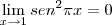
Essas são as condições necessárias para aplicarmos a regra de L'Hopital, e devemos agora derivar as equações (as derivamos separadamente, não utilizamos aqui a regra do quociente), mas primeiro vamos arrumá-las:
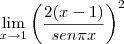

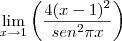
Comecemos a derivar:
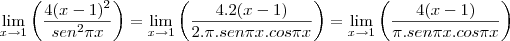
Agora vamos derivar mais uma vez (é importante prestar bastante atenção na derivada da função seno acima e na próxima em que deveremos aplicar a regra do produto):
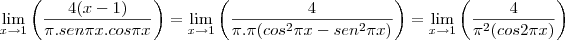
Finalmente:
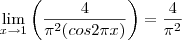
Obs: É importante lembrar que para podermos continuar derivando como fizemos nesse exercício a 1ª condição (a de que f(x)/g(x) seja uma indeterminação) seja satisfeita também para a derivada, como é o caso aqui.
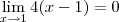
;
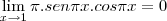
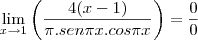
Caso tenha dúvidas sobre algum procedimento usado, me diga! Até a próxima.
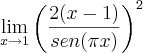
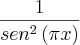 , por uma infinitésima cujo limite vai a zero,
, por uma infinitésima cujo limite vai a zero, ![{\left[2\left(x-1 \right) \right]}^{2} {\left[2\left(x-1 \right) \right]}^{2}](/latexrender/pictures/6a713ab7063e6073d745a9a6f86e1fb9.png) . Só que para minha surpresa, no gabarito a resposta é
. Só que para minha surpresa, no gabarito a resposta é 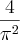 . Como eu chegaria a essa resposta? Não faço a mínima ideia.
. Como eu chegaria a essa resposta? Não faço a mínima ideia.


![\lim_{x\rightarrow 1} [2(x-1)]^2 = 0 \lim_{x\rightarrow 1} [2(x-1)]^2 = 0](/latexrender/pictures/c19f117c05ecb459a3a05058f61d382a.png) ;
; 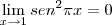
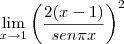

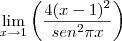
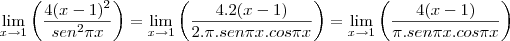
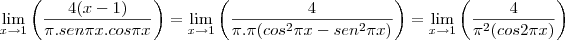
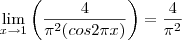
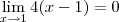 ;
; 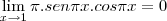
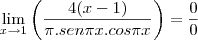
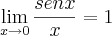 .
. 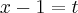 , temos que
, temos que 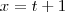 . E se
. E se 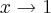 , então
, então 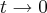 . Substituindo
. Substituindo  por
por  , e
, e  por
por  , ficamos com:
, ficamos com:![\lim_{x\rightarrow1} {\left[\frac{2\left(x-1 \right)}{sen\left(\pi x \right)} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen\left[\pi \left(t+1 \right) \right] \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen \left(\pi t+\pi \right)} \right]}^{2} = \lim_{x\rightarrow1} {\left[\frac{2\left(x-1 \right)}{sen\left(\pi x \right)} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen\left[\pi \left(t+1 \right) \right] \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen \left(\pi t+\pi \right)} \right]}^{2} =](/latexrender/pictures/a84fa756da823cceeed5cae020618f78.png)
![=\lim_{t\rightarrow0} {\left[\frac{2t}{sen \pi t.cos\pi+sen \pi .cos\pi t} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{-sen\pi t} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2t.\pi}{\left(-sen\pi t \right).\pi} \right]^{2} = =\lim_{t\rightarrow0} {\left[\frac{2t}{sen \pi t.cos\pi+sen \pi .cos\pi t} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{-sen\pi t} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2t.\pi}{\left(-sen\pi t \right).\pi} \right]^{2} =](/latexrender/pictures/7c7520eaebb9360046cbdfc1d121ba97.png)
![=\lim_{t\rightarrow0} \left[\frac{2\pi t}{\left(-sen\pi t \right).\pi} \right]^{2} = \lim_{t\rightarrow0} {\left[\frac{\pi t}{sen \pi t} . \frac{2}{\left(-\pi \right)} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2}{-\pi} \right]^2 = \frac{4}{{\pi}^{2}} =\lim_{t\rightarrow0} \left[\frac{2\pi t}{\left(-sen\pi t \right).\pi} \right]^{2} = \lim_{t\rightarrow0} {\left[\frac{\pi t}{sen \pi t} . \frac{2}{\left(-\pi \right)} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2}{-\pi} \right]^2 = \frac{4}{{\pi}^{2}}](/latexrender/pictures/52829ff3c16e0a8b4602b13a92a8db1e.png) .
.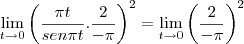
 (que não pode ser simplesmente cortada). Se falares do limite trigonométrico fundamental, ele é
(que não pode ser simplesmente cortada). Se falares do limite trigonométrico fundamental, ele é 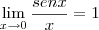 e não
e não 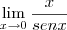 (se observar a definição do limite trigonométrico, verá como nesse caso a função não tende a 1). E então como é isso?
(se observar a definição do limite trigonométrico, verá como nesse caso a função não tende a 1). E então como é isso? 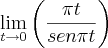
 , concorda? Aí ficamos com:
, concorda? Aí ficamos com:![\lim_{t\rightarrow0} \left(\frac{\pi t}{sen\pi t} \right) = \lim_{\pi t\rightarrow0} \left(\frac{\pi t}{sen \pi t} \right) = \lim_{\pi t\rightarrow0} \left[\frac{1}{\frac{sen \pi t}{\pi t}} \right] = \frac{1}{1} = 1 \lim_{t\rightarrow0} \left(\frac{\pi t}{sen\pi t} \right) = \lim_{\pi t\rightarrow0} \left(\frac{\pi t}{sen \pi t} \right) = \lim_{\pi t\rightarrow0} \left[\frac{1}{\frac{sen \pi t}{\pi t}} \right] = \frac{1}{1} = 1](/latexrender/pictures/9e18dd484cacc55ac20ac627096623cd.png) .
.