-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478167 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 531769 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495308 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 705550 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2121351 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por johnatta » Dom Nov 22, 2015 11:40
por johnatta » Dom Nov 22, 2015 11:40
Mostre que a equação tem exatamente uma raiz real
a- 2x+ cosx=0 b-x³ +e^x=0
Nota- nao sei nem como inicia
-
johnatta
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Ter Abr 07, 2015 17:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Qua Nov 25, 2015 16:40
por adauto martins » Qua Nov 25, 2015 16:40
para resolver essa questao usaremos 'REGRA DOS SINAIS DE DESCARTES" e aproximaçao de uma serie de taylor de um polinomio,nao é muito preciso,mas é o q. podemos usar...
a)

,aqui vamos tomar a menor potencia menor ou igual a potencia do polinomio em questao,no caso x...logo...
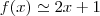
,pois
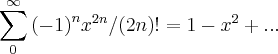
...utilizando a regra de descartes p/raizes teremos...
nenhuma mudança de sinal p/x positivo e
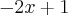
,uma mudança p/x negativo...logo existe uma unica raiz real,e negativa p/f(x)...
b)

...vamos tomar entao:

...usando a regra de descartes,nao ha troca de sinais dos coeficientes de f(x) p/x positivo...p/x negativo,existem duas trocas de sinais....como f(x) é um polinomio de grau igual a tres deveriamos ter tres raizes(reais ou complexas),o q. nos leva a deduzir q. existe uma raioz real negativa e duas raizes complexas(conjugadas)...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Derivadas)- Cálculo A
 por Matheus1999 » Seg Jan 25, 2021 14:15
por Matheus1999 » Seg Jan 25, 2021 14:15
- 1 Respostas
- 5185 Exibições
- Última mensagem por DanielFerreira

Sex Abr 02, 2021 18:23
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Derivadas sucessivas
por karenfreitas » Sáb Mai 28, 2016 11:00
- 2 Respostas
- 3502 Exibições
- Última mensagem por nakagumahissao

Seg Mai 30, 2016 23:18
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2] derivadas parciais
 por NavegantePI » Sáb Jun 25, 2016 18:08
por NavegantePI » Sáb Jun 25, 2016 18:08
- 1 Respostas
- 2472 Exibições
- Última mensagem por adauto martins

Seg Jun 27, 2016 12:22
Cálculo: Limites, Derivadas e Integrais
-
- [cálculo de derivadas] Ajuda em exercicio
por Ljoe » Ter Jul 12, 2011 12:49
- 3 Respostas
- 2453 Exibições
- Última mensagem por Fabio Cabral

Qua Jul 13, 2011 10:52
Cálculo: Limites, Derivadas e Integrais
-
- [cálculo de derivadas de funções modulares]
por letciabr7 » Sáb Mai 09, 2015 16:44
- 1 Respostas
- 1748 Exibições
- Última mensagem por adauto martins

Seg Mai 11, 2015 16:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 63 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ,aqui vamos tomar a menor potencia menor ou igual a potencia do polinomio em questao,no caso x...logo...
,aqui vamos tomar a menor potencia menor ou igual a potencia do polinomio em questao,no caso x...logo...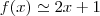 ,pois
,pois 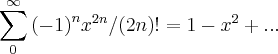 ...utilizando a regra de descartes p/raizes teremos...
...utilizando a regra de descartes p/raizes teremos...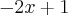 ,uma mudança p/x negativo...logo existe uma unica raiz real,e negativa p/f(x)...
,uma mudança p/x negativo...logo existe uma unica raiz real,e negativa p/f(x)... ...vamos tomar entao:
...vamos tomar entao: ...usando a regra de descartes,nao ha troca de sinais dos coeficientes de f(x) p/x positivo...p/x negativo,existem duas trocas de sinais....como f(x) é um polinomio de grau igual a tres deveriamos ter tres raizes(reais ou complexas),o q. nos leva a deduzir q. existe uma raioz real negativa e duas raizes complexas(conjugadas)...
...usando a regra de descartes,nao ha troca de sinais dos coeficientes de f(x) p/x positivo...p/x negativo,existem duas trocas de sinais....como f(x) é um polinomio de grau igual a tres deveriamos ter tres raizes(reais ou complexas),o q. nos leva a deduzir q. existe uma raioz real negativa e duas raizes complexas(conjugadas)...