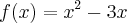 e que seja perpendicular à reta
e que seja perpendicular à reta 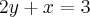 .
.nem sei por onde começar to perdido, so preciso saber como se faz.
desde ja agradeço

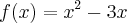 e que seja perpendicular à reta
e que seja perpendicular à reta 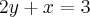 .
.





Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

