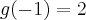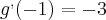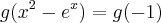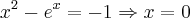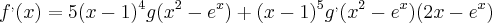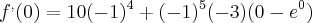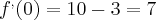por juflamanto » Sáb Out 10, 2015 21:10
por juflamanto » Sáb Out 10, 2015 21:10
Resolvendo essa questão, eu somente derivei f e encontrei f'(0)=-4 e nao usei esse g.A minha dúvida é essa, pra serve esse g(-1) e g'(-1)?
- Anexos
-
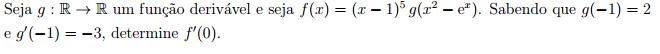
- 1.JPG (7.59 KiB) Exibido 2751 vezes
-
juflamanto
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Ago 07, 2015 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: fisica
- Andamento: cursando
 por nakagumahissao » Qua Out 14, 2015 16:55
por nakagumahissao » Qua Out 14, 2015 16:55
Sabe-se que:
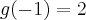
e
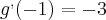
Para que :
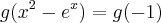
Precisaremos necessariamente ter que:
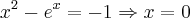
Derivando-se f(x) tem-se que:

Pela regra da cadeia:
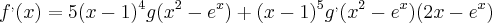
Usando os valores dados no resultado acima, tem-se:
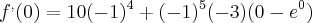
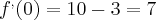
Se não me engano, é isso.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por gilijgs » Qui Out 15, 2015 16:06
por gilijgs » Qui Out 15, 2015 16:06
Olá pessoal aproveitando o Titulo derivadas, costaria da ajuda para responder a pergunta abaixo.
derivadas parciais:
Um modelo para área da superfície do corpo humano é dado pela função S(W,H) = 0,109W^0,425 H^0,725, onde W é o peso (em libras), H é a altura em polegadas e S é a medida em pés quadrados.
a)Ache a sua área superficial em metros quadrados.
B)Ache ?s/?W e ?s/?H e interprete o resultado.
-
gilijgs
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Out 15, 2015 15:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10886 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13191 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14795 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5113 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.