Tentei resolver as questões utilizando apenas os residuos das singularidades reais, que estavam dentro do contorno, mas as respostas não conferem para nenhuma.
Segue abaixo alguns exemplos e minha tentativa de resolução:
Integrais que normalmente apareciam:
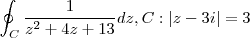
Integrais que estou tendo problemas:
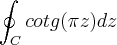 C é o retangulo definido por x=\frac{1}{2},x=\pi ,y=-1,y=1
C é o retangulo definido por x=\frac{1}{2},x=\pi ,y=-1,y=1Tentativa de resolução:
Singularidades reais dentro do contorno: z=1 , z=2 , z=3
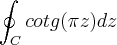 =
= 
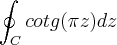 =
= (
( 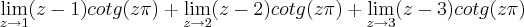 )
)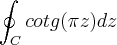 =
= 
No entanto a resposta certa é 6i. Por que?
Se alguem puder me ajudar, agradeço.
Ps.: Tenho mais exemplos se alguem precisar.


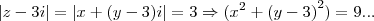
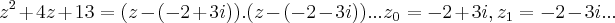
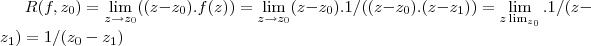
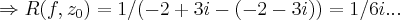 ...o mesmo raciocinio se aplica ao polo
...o mesmo raciocinio se aplica ao polo 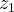 ,q. tera
,q. tera 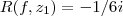 ...logo o valor da integral sera...
...logo o valor da integral sera...
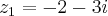 nao esta dentro da regiao de integraçao...logo...
nao esta dentro da regiao de integraçao...logo...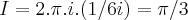 ...obrigado...
...obrigado... .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
