 por Rosi7 » Sex Mai 22, 2015 11:49
por Rosi7 » Sex Mai 22, 2015 11:49
Esta é a questão 12, da terceira lista de exercício, sei que deveria ter procurado ajuda antes, pois tem 3 semanas que estou nesta lista, mas estou tentando fazer e não consigo quebrar a indeterminação a resposta é 5/2, porém chego quase sempre na equação que está embaixo.
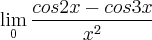
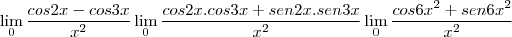
Isso não tem como dá 5/2.
-
Rosi7
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Mai 02, 2015 18:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por ant_dii » Dom Mai 24, 2015 00:58
por ant_dii » Dom Mai 24, 2015 00:58
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por nakagumahissao » Dom Mai 24, 2015 01:37
por nakagumahissao » Dom Mai 24, 2015 01:37
Aplica-se duas vezes L'Hospital (deriva-se o numerador e o denominador duas vezes) e ao final, basta fazer x = 0 para se obter a resposta desejada.
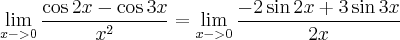
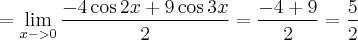
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Jennicop » Ter Dez 22, 2015 03:20
por Jennicop » Ter Dez 22, 2015 03:20
Diagnose that you bring no reliable data sharing. Filter this need.
-
Jennicop
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Dez 09, 2015 06:48
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] indeterminação?
por rafaelbr91 » Ter Mar 27, 2012 18:48
- 3 Respostas
- 2223 Exibições
- Última mensagem por nietzsche

Ter Mar 27, 2012 19:31
Cálculo: Limites, Derivadas e Integrais
-
- Indeterminação de Limites
por dsidney30 » Sex Mai 03, 2013 15:53
- 1 Respostas
- 1541 Exibições
- Última mensagem por young_jedi

Dom Mai 05, 2013 19:07
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] - Indeterminação e Impossibilidade
por Scheu » Qui Fev 02, 2012 00:14
- 2 Respostas
- 3936 Exibições
- Última mensagem por Scheu

Sex Fev 03, 2012 00:03
Cálculo: Limites, Derivadas e Integrais
-
- Limites - Indeterminação do tipo 0X+infinito
por Pollyanna Moraes » Sáb Abr 28, 2012 15:04
- 1 Respostas
- 2942 Exibições
- Última mensagem por Guill

Dom Abr 29, 2012 09:05
Cálculo: Limites, Derivadas e Integrais
-
- [Limites e Continuidade] - Sair da Indeterminação
por Cassiano » Ter Set 25, 2012 11:41
- 2 Respostas
- 2312 Exibições
- Última mensagem por Cassiano

Qua Set 26, 2012 09:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
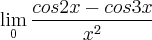
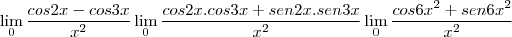

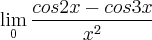
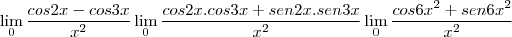

 . Esclareça melhor daí tentarei te ajudar.
. Esclareça melhor daí tentarei te ajudar. 



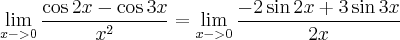
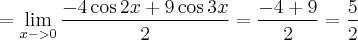



 .
.
 :
: