 por neoreload » Sex Mar 20, 2015 07:04
por neoreload » Sex Mar 20, 2015 07:04
Pessoal como resolver essa :
Encontrar o comprimento de arco da curva:

até
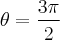
resposta:
![\frac{\sqrt[]{5}({e}^{3x}-1)}{2} \frac{\sqrt[]{5}({e}^{3x}-1)}{2}](/latexrender/pictures/857df040c666599e93d1c6a1090894eb.png)
Estou bem no inicio, se puderem colocar o passo a passo bem detalhado eu agradeceria

. E se não for exagerar, fazer da forma mais fácil que puder, pq ta dificil pra aprender

-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por neoreload » Dom Mar 22, 2015 23:16
por neoreload » Dom Mar 22, 2015 23:16
neoreload escreveu:Pessoal como resolver essa :
Encontrar o comprimento de arco da curva:

até
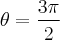
resposta:
![\frac{\sqrt[]{5}({e}^{3x}-1)}{2} \frac{\sqrt[]{5}({e}^{3x}-1)}{2}](/latexrender/pictures/857df040c666599e93d1c6a1090894eb.png)
Estou bem no inicio, se puderem colocar o passo a passo bem detalhado eu agradeceria

. E se não for exagerar, fazer da forma mais fácil que puder, pq ta dificil pra aprender

alguém ? :(
-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Seg Mar 23, 2015 01:55
por Russman » Seg Mar 23, 2015 01:55
É possível mostrar que o comprimento L de um arco
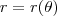
definido entre
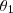
e

é
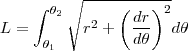
Tente prosseguir.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] para calcular volume
por neoreload » Sex Nov 21, 2014 05:26
- 1 Respostas
- 4619 Exibições
- Última mensagem por felipederaldino

Qua Nov 26, 2014 11:16
Cálculo: Limites, Derivadas e Integrais
-
- Integral para calcular o volume
por neoreload » Sex Mar 13, 2015 05:11
- 1 Respostas
- 4085 Exibições
- Última mensagem por Russman

Sex Mar 13, 2015 17:00
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda para Calcular uma Integral Gaussiana
por Luthius » Qui Jul 12, 2018 09:22
- 0 Respostas
- 4350 Exibições
- Última mensagem por Luthius

Qui Jul 12, 2018 09:22
Cálculo: Limites, Derivadas e Integrais
-
- [Comprimento de Arco] Deduzir funções para Integrar
 por Mendes » Dom Ago 23, 2015 15:10
por Mendes » Dom Ago 23, 2015 15:10
- 0 Respostas
- 1436 Exibições
- Última mensagem por Mendes

Dom Ago 23, 2015 15:10
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3701 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 até
até 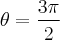
![\frac{\sqrt[]{5}({e}^{3x}-1)}{2} \frac{\sqrt[]{5}({e}^{3x}-1)}{2}](/latexrender/pictures/857df040c666599e93d1c6a1090894eb.png)
 . E se não for exagerar, fazer da forma mais fácil que puder, pq ta dificil pra aprender
. E se não for exagerar, fazer da forma mais fácil que puder, pq ta dificil pra aprender 
 até
até 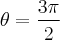
![\frac{\sqrt[]{5}({e}^{3x}-1)}{2} \frac{\sqrt[]{5}({e}^{3x}-1)}{2}](/latexrender/pictures/857df040c666599e93d1c6a1090894eb.png)
 . E se não for exagerar, fazer da forma mais fácil que puder, pq ta dificil pra aprender
. E se não for exagerar, fazer da forma mais fácil que puder, pq ta dificil pra aprender 
até
. E se não for exagerar, fazer da forma mais fácil que puder, pq ta dificil pra aprender

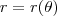 definido entre
definido entre 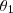 e
e  é
é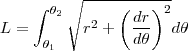


 .
.



