 por lucassouza » Qua Fev 18, 2015 00:19
por lucassouza » Qua Fev 18, 2015 00:19
tem duas questões que não consegui desenvolver.... a primeira a resposta dá zero a segunda se não me engano dá -1/2( não lembro)... não consegui desenvolver a segunda por conta desse seno e cosseno que aparece. a primeira está na imagem.
- Anexos
-

-
lucassouza
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Set 15, 2014 15:03
- Formação Escolar: SUPLETIVO
- Andamento: cursando
 por adauto martins » Qui Fev 19, 2015 15:20
por adauto martins » Qui Fev 19, 2015 15:20
a)como
![{x}^{2}\succ \sqrt[]{x}\Rightarrow \lim_{x\rightarrow \infty}\sqrt[]{x}/{x}^{2}=0 {x}^{2}\succ \sqrt[]{x}\Rightarrow \lim_{x\rightarrow \infty}\sqrt[]{x}/{x}^{2}=0](/latexrender/pictures/5f2547b7142eaecaf5c3cce53fe41d75.png)
b)I=

=
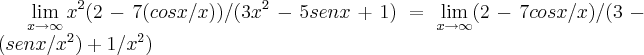
,como
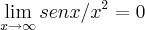
,pois o numerador varia de
![[-1,1] [-1,1]](/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png)
e o denominador cresce indefinidamente,assim tbem eh

,logo...
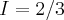
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por lucassouza » Dom Fev 22, 2015 22:44
por lucassouza » Dom Fev 22, 2015 22:44
Grato man!
-
lucassouza
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Set 15, 2014 15:03
- Formação Escolar: SUPLETIVO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5408 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4753 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4779 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4807 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2792 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![{x}^{2}\succ \sqrt[]{x}\Rightarrow \lim_{x\rightarrow \infty}\sqrt[]{x}/{x}^{2}=0 {x}^{2}\succ \sqrt[]{x}\Rightarrow \lim_{x\rightarrow \infty}\sqrt[]{x}/{x}^{2}=0](/latexrender/pictures/5f2547b7142eaecaf5c3cce53fe41d75.png)
 =
=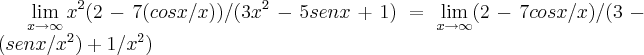 ,como
,como 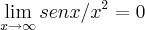 ,pois o numerador varia de
,pois o numerador varia de ![[-1,1] [-1,1]](/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) e o denominador cresce indefinidamente,assim tbem eh
e o denominador cresce indefinidamente,assim tbem eh  ,logo...
,logo...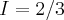



 .
.
 :
: