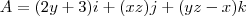 , calcular
, calcular  ao longo das retas que ligam sucessivamente os pontos (0,0,0) , (0,0,1) , (0,1,1) , (2,1,1)
ao longo das retas que ligam sucessivamente os pontos (0,0,0) , (0,0,1) , (0,1,1) , (2,1,1)Resp: 10
Como fazer ?
Obrigado !!

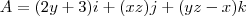 , calcular
, calcular  ao longo das retas que ligam sucessivamente os pontos (0,0,0) , (0,0,1) , (0,1,1) , (2,1,1)
ao longo das retas que ligam sucessivamente os pontos (0,0,0) , (0,0,1) , (0,1,1) , (2,1,1)
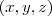 então a a integral de linha terá um valor independente do caminho. Infelizmente, não é o caso. Então, primeiramente, calcule o produto interno
então a a integral de linha terá um valor independente do caminho. Infelizmente, não é o caso. Então, primeiramente, calcule o produto interno  onde
onde 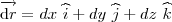 .
. .
.
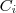 é a reta que liga os pontos consecutivos.
é a reta que liga os pontos consecutivos. 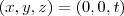 .
.![\int_{C_1} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{1} \left [(2y(t)+3) dx(t) + x(t)z(t) dy(t) + (y(t)z(t)-x(t)) dz(t) \right ] = 0 \int_{C_1} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{1} \left [(2y(t)+3) dx(t) + x(t)z(t) dy(t) + (y(t)z(t)-x(t)) dz(t) \right ] = 0](/latexrender/pictures/ce74f329fd5cbc8147f24173fc44095f.png) .
.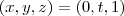 de modo que a integral C_2 também será nula.
de modo que a integral C_2 também será nula.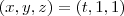 de modo que
de modo que ![\int_{C_3} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{2} \left [(2y(t)+3)\ dx(t) + x(t)z(t) \ dy(t) + (y(t)z(t)-x(t)) \ dz(t) \right ] = \int_{C_3} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{2} \left [(2y(t)+3)\ dx(t) + x(t)z(t) \ dy(t) + (y(t)z(t)-x(t)) \ dz(t) \right ] =](/latexrender/pictures/ab052c79629b01233e8ffd8b33b0ef33.png)
 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 19 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.