 por Fernandobertolaccini » Ter Fev 03, 2015 12:43
por Fernandobertolaccini » Ter Fev 03, 2015 12:43
Se
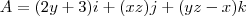
, calcular

ao longo das retas que ligam sucessivamente os pontos (0,0,0) , (0,0,1) , (0,1,1) , (2,1,1)
Resp: 10
Como fazer ?
Obrigado !!
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por Russman » Ter Fev 03, 2015 19:07
por Russman » Ter Fev 03, 2015 19:07
O primeiro passo é calcular o rotacional do campo vetorial em questão. Se o mesmo for nulo para qualquer ponto
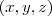
então a a integral de linha terá um valor independente do caminho. Infelizmente, não é o caso. Então, primeiramente, calcule o produto interno

onde
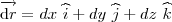
.
Obteremos

.
Agora, o caminho é dividido em 3 partes. Assim,

onde cada caminho
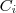
é a reta que liga os pontos consecutivos.
Como as retas são em 3D o melhor caminho é parametrizá-las. A primeira, deve passar por (0,0,0) e (0,0,1). Assim, uma boa parametrização seria
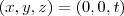
.
Daí,
![\int_{C_1} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{1} \left [(2y(t)+3) dx(t) + x(t)z(t) dy(t) + (y(t)z(t)-x(t)) dz(t) \right ] = 0 \int_{C_1} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{1} \left [(2y(t)+3) dx(t) + x(t)z(t) dy(t) + (y(t)z(t)-x(t)) dz(t) \right ] = 0](/latexrender/pictures/ce74f329fd5cbc8147f24173fc44095f.png)
.
A parametrização para o próximo caminho pode ser
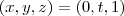
de modo que a integral C_2 também será nula.
Já para o caminho C_3 temos
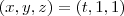
de modo que
![\int_{C_3} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{2} \left [(2y(t)+3)\ dx(t) + x(t)z(t) \ dy(t) + (y(t)z(t)-x(t)) \ dz(t) \right ] = \int_{C_3} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{2} \left [(2y(t)+3)\ dx(t) + x(t)z(t) \ dy(t) + (y(t)z(t)-x(t)) \ dz(t) \right ] =](/latexrender/pictures/ab052c79629b01233e8ffd8b33b0ef33.png)

.
O único caminho que contribui para a integral é o último.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo vetorial, integrais de linha e Teorema de green
 por Fernandobertolaccini » Qui Jun 11, 2015 20:19
por Fernandobertolaccini » Qui Jun 11, 2015 20:19
- 0 Respostas
- 2299 Exibições
- Última mensagem por Fernandobertolaccini

Qui Jun 11, 2015 20:19
Cálculo: Limites, Derivadas e Integrais
-
- Integral de linha - Trabalho
 por Bruhh » Ter Jul 05, 2011 16:55
por Bruhh » Ter Jul 05, 2011 16:55
- 1 Respostas
- 3319 Exibições
- Última mensagem por LuizAquino

Ter Jul 05, 2011 19:10
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Integral de linha
por pedro22132938 » Sex Dez 30, 2016 01:28
- 3 Respostas
- 7097 Exibições
- Última mensagem por adauto martins

Seg Jan 02, 2017 15:14
Cálculo: Limites, Derivadas e Integrais
-
- dúvida de cálculo 3 - integral de linha
por peridotito » Sex Nov 20, 2020 22:26
- 0 Respostas
- 5847 Exibições
- Última mensagem por peridotito

Sex Nov 20, 2020 22:26
Cálculo: Limites, Derivadas e Integrais
-
- Notação Calculo Combinatorio
por joaofonseca » Qua Jan 11, 2012 20:36
- 3 Respostas
- 1966 Exibições
- Última mensagem por Arkanus Darondra

Qua Jan 11, 2012 21:49
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
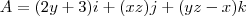 , calcular
, calcular  ao longo das retas que ligam sucessivamente os pontos (0,0,0) , (0,0,1) , (0,1,1) , (2,1,1)
ao longo das retas que ligam sucessivamente os pontos (0,0,0) , (0,0,1) , (0,1,1) , (2,1,1)
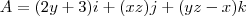 , calcular
, calcular  ao longo das retas que ligam sucessivamente os pontos (0,0,0) , (0,0,1) , (0,1,1) , (2,1,1)
ao longo das retas que ligam sucessivamente os pontos (0,0,0) , (0,0,1) , (0,1,1) , (2,1,1)
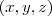 então a a integral de linha terá um valor independente do caminho. Infelizmente, não é o caso. Então, primeiramente, calcule o produto interno
então a a integral de linha terá um valor independente do caminho. Infelizmente, não é o caso. Então, primeiramente, calcule o produto interno  onde
onde 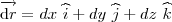 .
. .
.
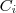 é a reta que liga os pontos consecutivos.
é a reta que liga os pontos consecutivos. 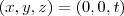 .
.![\int_{C_1} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{1} \left [(2y(t)+3) dx(t) + x(t)z(t) dy(t) + (y(t)z(t)-x(t)) dz(t) \right ] = 0 \int_{C_1} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{1} \left [(2y(t)+3) dx(t) + x(t)z(t) dy(t) + (y(t)z(t)-x(t)) dz(t) \right ] = 0](/latexrender/pictures/ce74f329fd5cbc8147f24173fc44095f.png) .
.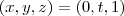 de modo que a integral C_2 também será nula.
de modo que a integral C_2 também será nula.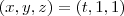 de modo que
de modo que ![\int_{C_3} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{2} \left [(2y(t)+3)\ dx(t) + x(t)z(t) \ dy(t) + (y(t)z(t)-x(t)) \ dz(t) \right ] = \int_{C_3} \overrightarrow{A} \cdot \overrightarrow{ \mathrm{d}r} = \int_{0}^{2} \left [(2y(t)+3)\ dx(t) + x(t)z(t) \ dy(t) + (y(t)z(t)-x(t)) \ dz(t) \right ] =](/latexrender/pictures/ab052c79629b01233e8ffd8b33b0ef33.png)
 .
.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.