 por natanaelskt » Sex Nov 28, 2014 21:09
por natanaelskt » Sex Nov 28, 2014 21:09
eai pessoal,tudo bem? alguém pode me ajudar nesta dúvida teórica?
a-) encontre a direção que cresce mais rapidamente da função f(x,y) = ((x^2)/2)+ (y^2)/2) no ponto(1,1).
eu fiz assim,mas não entendo porque meu raciocínio ta errado.
f(x,y) = ((x^2)/2)+ (y^2)/2)
grad f = (1,1)
Duf = grad f * u
mas grad f*u = |grad f| * |u| * cosB e cosB é zero(maior crescimento)
|u| = 1 (vetor unitario)
assim: u = |grad f| / grad f assim eu acharia u e depois eu só jogava na formula Duf = grad f * u e dava a direção.(paralelo a grad f).
mas no livro tá diferente,ta assim: u = grad f / |grad f|
-
natanaelskt
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Seg Mar 11, 2013 15:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por adauto martins » Sáb Nov 29, 2014 12:13
por adauto martins » Sáb Nov 29, 2014 12:13
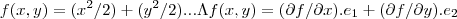
,onde
{

} e a base canonica do
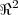
e

e o gradiente de f(x,y)...
entao:
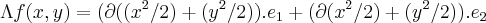
=

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- CALCULO 3 GRADIENTE E DERIVADA DIRECIONAL
por eduardo ifba » Dom Mai 14, 2017 20:05
- 0 Respostas
- 2968 Exibições
- Última mensagem por eduardo ifba

Dom Mai 14, 2017 20:05
Cálculo: Limites, Derivadas e Integrais
-
- [Gradiente e derivada direcional]
por dulifs » Seg Out 31, 2011 15:22
- 2 Respostas
- 4882 Exibições
- Última mensagem por dulifs

Seg Out 31, 2011 18:14
Cálculo: Limites, Derivadas e Integrais
-
- Questão de derivada direcional e gradiente
por Cristiano Tavares » Dom Mai 29, 2011 11:25
- 2 Respostas
- 3800 Exibições
- Última mensagem por Cristiano Tavares

Dom Mai 29, 2011 19:35
Cálculo: Limites, Derivadas e Integrais
-
- Derivada direcional e gradiente(só corrigir)?
por miyasato » Qua Jun 17, 2015 13:35
- 1 Respostas
- 2720 Exibições
- Última mensagem por adauto martins

Qua Jun 17, 2015 20:41
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo2: Derivada Parcial] Plano tg, Vetor Gradiente
por Claudio Parana » Qua Fev 05, 2014 20:06
- 0 Respostas
- 1198 Exibições
- Última mensagem por Claudio Parana

Qua Fev 05, 2014 20:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


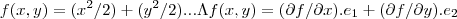 ,onde
,onde  } e a base canonica do
} e a base canonica do 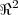 e
e  e o gradiente de f(x,y)...
e o gradiente de f(x,y)...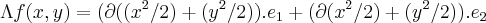 =
=


 .
.



