Um tanque de armazenamento de petróleo sofre uma ruptura em t = 0 e o petróleo vaza do tanque a uma taxa de
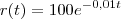 litros por minuto. Quanto petróleo vazou na primeira hora?
litros por minuto. Quanto petróleo vazou na primeira hora?Resposta = 4512L
Coloquei o tempo em 60minutos, e tentei fazer assim:
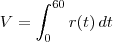 .
. 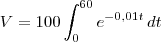 . Nessa parte fiz substituição e cheguei eim:
. Nessa parte fiz substituição e cheguei eim:![V=[\frac{100}{-0,01}\cdot e^{-0,01t}]_0^{60} V=[\frac{100}{-0,01}\cdot e^{-0,01t}]_0^{60}](/latexrender/pictures/28e321d7d5fe3c1d931c61ddd42de407.png)
![V=[-10000\cdot e^{-0,01t}]_0^{60} V=[-10000\cdot e^{-0,01t}]_0^{60}](/latexrender/pictures/e4d0b9e231ab2ac97aba77ff2aec958c.png)
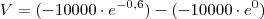
Ai que complicou, pq resolvendo isso, eu chego em
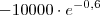 que da -5488. Bem diferente da resposta que é 4512. Percebi que se eu diminuir o -5488 de +10000 da a resposta. Mas de onde deveria vir os 10000? errei algo?
que da -5488. Bem diferente da resposta que é 4512. Percebi que se eu diminuir o -5488 de +10000 da a resposta. Mas de onde deveria vir os 10000? errei algo?

![\int_{0}^{60}100{e}^{-0,01t}.dt
100\int_{0}^{60}{e}^{-0,01t}.dt
100.{e}^{-0,01t}.\left(-100 \right)
-10000 \left[{e}^{\left(-0,01 \right)60} - {e}^{\left(-0,01 \right).0}\right]
-10000\left[-0,4512 \right]
r\left(60 \right) = 4512L \int_{0}^{60}100{e}^{-0,01t}.dt
100\int_{0}^{60}{e}^{-0,01t}.dt
100.{e}^{-0,01t}.\left(-100 \right)
-10000 \left[{e}^{\left(-0,01 \right)60} - {e}^{\left(-0,01 \right).0}\right]
-10000\left[-0,4512 \right]
r\left(60 \right) = 4512L](/latexrender/pictures/2e3822a2d643595c8d6a2345de132c35.png)


 .
.



