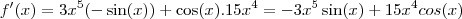por PORTER » Ter Nov 04, 2014 21:37
por PORTER » Ter Nov 04, 2014 21:37
ola, sou novo aqui no forum, gostaria de saber se na segunda ordem, tenho que derivar novamente o cos(x), estou fazendo assim:
:exercicio dado: f(x) = 3x5 . sen(x)
f'(x) = 15x^4 . cos(x)
f''(x) = 60x^3 . cos(x) <-- tem que derivar novamente ?
gostaria de saber se fiz o exercicio corretamente ou tem que derivar novamente o cos(x)
obrigado.
-
PORTER
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Nov 04, 2014 17:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por Russman » Ter Nov 04, 2014 22:02
por Russman » Ter Nov 04, 2014 22:02
Você precisa aplicar a regra da deriva do produto. Lembre-se que se uma função

é o priduto de outras duas, por exemplo,

e
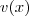
, isto é,
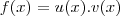
, então

A sua função
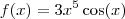
é, note que, o resultado do produto das funções

e

. Ou seja, na nossa notação anterior temos
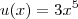
e
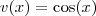
. Daí,
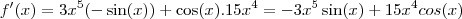
Agora, tente derivar novamente aplicando primeiro a regra da soma e depois a do produto novamente.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por PORTER » Qua Nov 05, 2014 10:11
por PORTER » Qua Nov 05, 2014 10:11
olá Russman, obrigado por responder, nesse caso, eu te pergundo, não teria que aplicar a regra de multiplicação, usando essa formula ?:
f'(x) = g'(x).h(x) + g(x) . h'(x)
= 15x^4 . cos(x) + 3x^5 . sen(x)
em seguida eu derivaria novamente.
obrigado.
-
PORTER
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Nov 04, 2014 17:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por Russman » Qua Nov 05, 2014 11:32
por Russman » Qua Nov 05, 2014 11:32
Sim. Foi exatamente essa fórmula que te escrevi. Mas cuidado com o sinal. A derivada da função cosseno é menos a seno.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- dúvida, derivar seno e cosseno até a terceira ordem
por PORTER » Qui Dez 11, 2014 08:10
- 1 Respostas
- 1348 Exibições
- Última mensagem por adauto martins

Sex Dez 12, 2014 11:34
Cálculo: Limites, Derivadas e Integrais
-
- EDO de Segunda Ordem
por OtavioBonassi » Ter Nov 15, 2011 11:45
- 0 Respostas
- 1258 Exibições
- Última mensagem por OtavioBonassi

Ter Nov 15, 2011 11:45
Sistemas de Equações
-
- como derivar até a terceira ordem
por PORTER » Qua Dez 10, 2014 09:52
- 1 Respostas
- 1639 Exibições
- Última mensagem por Cleyson007

Qua Dez 10, 2014 10:38
Cálculo: Limites, Derivadas e Integrais
-
- derivada de segunda ordem
por lgbmp » Sex Set 03, 2010 19:25
- 2 Respostas
- 3033 Exibições
- Última mensagem por lgbmp

Seg Set 06, 2010 13:35
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada de segunda ordem]
por spektroos » Sáb Nov 24, 2012 23:43
- 2 Respostas
- 2231 Exibições
- Última mensagem por spektroos

Dom Nov 25, 2012 02:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é o priduto de outras duas, por exemplo,
é o priduto de outras duas, por exemplo,  e
e 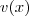 , isto é,
, isto é, 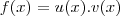 , então
, então
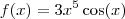 é, note que, o resultado do produto das funções
é, note que, o resultado do produto das funções  e
e  . Ou seja, na nossa notação anterior temos
. Ou seja, na nossa notação anterior temos 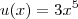 e
e 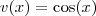 . Daí,
. Daí,