 por Fernandobertolaccini » Sáb Out 25, 2014 09:57
por Fernandobertolaccini » Sáb Out 25, 2014 09:57
A lei de Boyle para os gases afirma que P.V=k, onde P é a pressão, V é o volume e k é uma constante que depende do numero de moles do gás em questão e de sua temperatura.
Suponhamos que no instante t(minutos), a pressão seja dada por P(t) = 20 + 2t, com
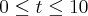
. Se em t=0 o volume é de 60cm³, determine a taxa de variação do volume por unidade de variação do tempo quando T=5.
Valeew !!
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por adauto martins » Sáb Out 25, 2014 11:42
por adauto martins » Sáb Out 25, 2014 11:42
taxa de variaçao de uma quantidade e dada pela derivada dessa quantidade em funçao do parametro a qual depende a quantidade,no caso V=V(t)...entao:dV/dt...pela equaçao de P=P(t),teremos:P=k/V...k/V(t)=20+2t...V(t)=k/(20+2t)...
dV/dt=2.k.ln(20+2t)...t=0,tem-se 60=2kln(20)...aqui acha-se k e depois,calcula-se V,para T=5...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Fernandobertolaccini » Sáb Out 25, 2014 11:57
por Fernandobertolaccini » Sáb Out 25, 2014 11:57
A resposta seria: 0,33 cm³ ??
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por Fernandobertolaccini » Sáb Out 25, 2014 12:12
por Fernandobertolaccini » Sáb Out 25, 2014 12:12
adauto martins escreveu:taxa de variaçao de uma quantidade e dada pela derivada dessa quantidade em funçao do parametro a qual depende a quantidade,no caso V=V(t)...entao:dV/dt...pela equaçao de P=P(t),teremos:P=k/V...k/V(t)=20+2t...V(t)=k/(20+2t)...
dV/dt=2.k.ln(20+2t)...t=0,tem-se 60=2kln(20)...aqui acha-se k e depois,calcula-se V,para T=5...
A resposta seria: 0,33 cm³ ??
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por adauto martins » Sáb Out 25, 2014 12:21
por adauto martins » Sáb Out 25, 2014 12:21
dV/dt=2(30/ln(20)).ln(20+2t)=60.ln(20+2t-20)=60.ln(2t)...p/t=5,teriamos:
dV/dt=60.ln(10)=60.(2,3)=138

,t(unidade de tempo)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Fernandobertolaccini » Sáb Out 25, 2014 12:45
por Fernandobertolaccini » Sáb Out 25, 2014 12:45
adauto martins escreveu:dV/dt=2(30/ln(20)).ln(20+2t)=60.ln(20+2t-20)=60.ln(2t)...p/t=5,teriamos:
dV/dt=60.ln(10)=60.(2,3)=138

,t(unidade de tempo)
Obrigado !!
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Taxas Relacionadas]
por Ana_Rodrigues » Seg Nov 14, 2011 10:02
- 2 Respostas
- 4593 Exibições
- Última mensagem por LuizAquino

Seg Nov 14, 2011 12:19
Cálculo: Limites, Derivadas e Integrais
-
- Taxas Relacionadas
por RonnieAlmeida » Qui Mai 22, 2014 16:48
- 0 Respostas
- 1462 Exibições
- Última mensagem por RonnieAlmeida

Qui Mai 22, 2014 16:48
Cálculo: Limites, Derivadas e Integrais
-
- Taxas Relacionadas
por RonnieAlmeida » Qui Mai 22, 2014 16:58
- 1 Respostas
- 2710 Exibições
- Última mensagem por alienante

Dom Jun 15, 2014 07:59
Cálculo: Limites, Derivadas e Integrais
-
- Taxas relacionadas
por Lorijuca » Qui Mai 29, 2014 22:23
- 0 Respostas
- 2954 Exibições
- Última mensagem por Lorijuca

Qui Mai 29, 2014 22:23
Cálculo: Limites, Derivadas e Integrais
-
- TAXAS RELACIONADAS
por Daniela[ » Sáb Jul 05, 2014 15:15
- 3 Respostas
- 6976 Exibições
- Última mensagem por young_jedi

Dom Jul 06, 2014 14:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
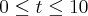 . Se em t=0 o volume é de 60cm³, determine a taxa de variação do volume por unidade de variação do tempo quando T=5.
. Se em t=0 o volume é de 60cm³, determine a taxa de variação do volume por unidade de variação do tempo quando T=5. 
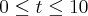 . Se em t=0 o volume é de 60cm³, determine a taxa de variação do volume por unidade de variação do tempo quando T=5.
. Se em t=0 o volume é de 60cm³, determine a taxa de variação do volume por unidade de variação do tempo quando T=5. 



 ,t(unidade de tempo)
,t(unidade de tempo)
,t(unidade de tempo)


 .
.



