 por D_Honda » Qui Jan 07, 2010 23:22
por D_Honda » Qui Jan 07, 2010 23:22
Olá!
Inicialmente, gostaria de dizer que sou novo neste fórum.
Muito gostei desse ambiente propicio ao estudo, principalmente na internet, ambiente tão suscetível à outras atividas tão diversas.
Pois bem, meu professor de Cálculo I deixou 7 exercícios interessantes de limites. O curso terminou e não deu tempo dele resolver todos. Dos 7, consegui fazer 3. Gostaria da ajuda de vocês para tentar soluciona-los. Conforme formos resolvendo um, passo o outro.
Desde já agradeço a atenção e peço desculpas se a escrita matemática não ficar clara, é a primeira vez que uso essa linguagem em um computador.
O primeiro:
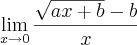
Tentei fazer o seguinte:

Mas continuamos com a indeterminação ( = 0 ) no denominador.
Obrigado.
Diego.
-
D_Honda
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jan 07, 2010 22:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Química
- Andamento: cursando
 por Molina » Sex Jan 08, 2010 13:36
por Molina » Sex Jan 08, 2010 13:36
Boa tarde, Diego.
Note que fazendo por esse processo do conjugado na parte do denominador não temos 0, pois x se aproxima de zero, mas nunca "chega" a ele... E cuidado ao usar o termo
indeterminação, pois será uma, quando tivermos

ou

.
Senão no caso de
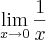
seria uma indeterminação também. Mas sabemos que isso tende ao infinito.
Vou ver se consigo resolver esta. Pensei por alguma troca de veriável, vamos ver.
Abraços e faça bom uso do fórum.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por D_Honda » Sex Jan 08, 2010 19:49
por D_Honda » Sex Jan 08, 2010 19:49
molina escreveu:Boa tarde, Diego.
Note que fazendo por esse processo do conjugado na parte do denominador não temos 0, pois x se aproxima de zero, mas nunca "chega" a ele... E cuidado ao usar o termo
indeterminação, pois será uma, quando tivermos

ou

.
Senão no caso de
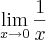
seria uma indeterminação também. Mas sabemos que isso tende ao infinito.
Vou ver se consigo resolver esta. Pensei por alguma troca de veriável, vamos ver.
Abraços e faça bom uso do fórum.

Eu tenho costume de usar o termo "indeterminação" quando aparece zero no denominador, caso esse que devemos evitar.
Quando disse que tinhamos um zero no denominador, é porque se substituirmos o valor que "x" tende no próprio x do denominador o mesmo tenderá a zero. Eu aprendi a fazer essa substituição para achar o valor do limite, mas não sei se apliquei bem. Todavia, obrigado pelo conselho.
Se achar a solução, compartilhe conosco.
Obrigado.
-
D_Honda
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jan 07, 2010 22:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Química
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites, help aqui
por Maykids » Dom Mar 20, 2011 13:00
- 3 Respostas
- 9905 Exibições
- Última mensagem por LuizAquino

Dom Mar 20, 2011 17:10
Cálculo: Limites, Derivadas e Integrais
-
- exercicio bem dificil preciso de uma maozinha
por Fabricio dalla » Ter Mar 15, 2011 15:21
- 5 Respostas
- 3244 Exibições
- Última mensagem por Fabricio dalla

Sáb Mar 19, 2011 20:38
Binômio de Newton
-
- Ajuda aqui!
por Liahtz » Sex Ago 07, 2015 17:38
- 1 Respostas
- 10903 Exibições
- Última mensagem por nakagumahissao

Sáb Ago 08, 2015 11:33
Matrizes e Determinantes
-
- ajuda aqui!
 por zenildo » Seg Mai 09, 2016 01:18
por zenildo » Seg Mai 09, 2016 01:18
- 5 Respostas
- 10412 Exibições
- Última mensagem por zenildo

Qui Mai 12, 2016 22:41
Trigonometria
-
- Auxilie aqui!!!!!
 por zenildo » Dom Jun 05, 2016 12:13
por zenildo » Dom Jun 05, 2016 12:13
- 2 Respostas
- 6935 Exibições
- Última mensagem por zenildo

Dom Jun 05, 2016 21:22
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
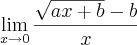



 ou
ou  .
.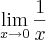 seria uma indeterminação também. Mas sabemos que isso tende ao infinito.
seria uma indeterminação também. Mas sabemos que isso tende ao infinito.






