-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480513 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 541138 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 504943 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 731781 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2172731 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por victornakaya » Sáb Jun 28, 2014 20:03
por victornakaya » Sáb Jun 28, 2014 20:03
[tex]F(x,y,z) = -{x}^{2}+ {x}_{sen z} + \frac{y}{{z}^{2}} + 1 = 0
Eu fiz desse jeito: df/dx = d0/dx = -2x + senz + x cos*z dz/dx + y/z*2 + 1 =0
A minha dúvida surgiu como faço para derivar y/z*2?
-
victornakaya
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Ago 21, 2013 21:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Sáb Jul 05, 2014 16:05
por young_jedi » Sáb Jul 05, 2014 16:05
você pode reescrever como
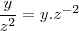
e utilizando regra da cadeia e do produto
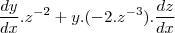
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivação Implicita
por xafabi » Qui Mai 02, 2013 13:56
- 0 Respostas
- 1134 Exibições
- Última mensagem por xafabi

Qui Mai 02, 2013 13:56
Cálculo: Limites, Derivadas e Integrais
-
- Derivação implicita.
por cardoed001 » Sáb Set 28, 2013 21:56
- 2 Respostas
- 2316 Exibições
- Última mensagem por cardoed001

Dom Set 29, 2013 12:28
Cálculo: Limites, Derivadas e Integrais
-
- Derivação Implicita
por victornakaya » Sáb Jun 28, 2014 20:03
- 0 Respostas
- 1017 Exibições
- Última mensagem por victornakaya

Sáb Jun 28, 2014 20:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivação implicita
por Carolminera » Dom Jul 06, 2014 23:07
- 1 Respostas
- 1103 Exibições
- Última mensagem por young_jedi

Seg Jul 07, 2014 20:07
Cálculo: Limites, Derivadas e Integrais
-
- Derivação implicita , quem ajuda ?
por Loretto » Ter Ago 03, 2010 02:15
- 4 Respostas
- 4690 Exibições
- Última mensagem por LuizAquino

Qua Mar 09, 2011 22:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 56 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



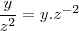
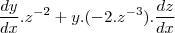


 .
.
 :
: