 e de
e de  . Determine r.
. Determine r.Nessa questão tive dificuldade, pois ele não me deu os pontos que a reta pedida passa. Qualquer ajuda é bem vinda!



 e de
e de  . Determine r.
. Determine r.


 a uma função qualquer
a uma função qualquer  .
.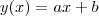 a reta tangente a
a reta tangente a  no ponto
no ponto  . Sabemos que a inclinação de r neste ponto será dada pela derivada da função aplicada no mesmo. Então, se
. Sabemos que a inclinação de r neste ponto será dada pela derivada da função aplicada no mesmo. Então, se 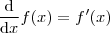 ,
, 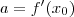 . Como a reta e a função compartilham a ordenada é preciso que
. Como a reta e a função compartilham a ordenada é preciso que 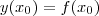 de onde
de onde  .
. .
.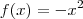 o ponto de tangência tem coordenadas
o ponto de tangência tem coordenadas 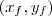 e para
e para  tem coordenadas
tem coordenadas 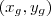 , então
, então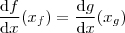
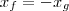 . Os pontos de tangência são simétricos. Tudo bem até aqui?
. Os pontos de tangência são simétricos. Tudo bem até aqui?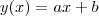 onde ,como já sabemos,
onde ,como já sabemos,  . Assim,
. Assim, 
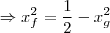
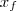 e
e 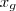 .
.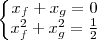
 . Assim, as retas tangentes são
. Assim, as retas tangentes são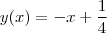
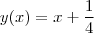



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
