 por cardoed001 » Dom Jun 08, 2014 17:49
por cardoed001 » Dom Jun 08, 2014 17:49
Boa tarde,
Alguém, por favor, poderia me explicar porque a integral
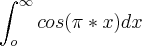
é divergente?
Eu cheguei na resposta:

(com limite superior b e inferior zero, para calcular a integral definida), mas não intendi porque ela diverge.
Muito obrigado.
-
cardoed001
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Set 15, 2013 00:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por e8group » Dom Jun 08, 2014 22:15
por e8group » Dom Jun 08, 2014 22:15
Justamente por que o último limite está oscilando entre -1 e 1 , e portanto tal limite não nos diz nada . Se tal limite convergisse para algum n°

, então nas diversas formas de

ir para

, estes limites tbm valeriam

.
Por exemplo, tome
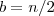
com

natural .
Note que

.
Verifique !
Ou seja, quanto n for suficiente grande b também o será e o resultado do limite poderá ser 0,1,-1 dependendo de n .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por cardoed001 » Dom Jun 08, 2014 22:39
por cardoed001 » Dom Jun 08, 2014 22:39
Muitíssimo obrigado,
Então essa oscilação faz com que a integral seja divergente.
Valeu mesmo.
-
cardoed001
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Dom Set 15, 2013 00:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integrais Impróprias
por menino de ouro » Qui Dez 20, 2012 13:32
- 2 Respostas
- 1919 Exibições
- Última mensagem por e8group

Sáb Dez 22, 2012 14:53
Cálculo: Limites, Derivadas e Integrais
-
- Integrais Impróprias
por menino de ouro » Seg Jan 28, 2013 20:03
- 2 Respostas
- 1535 Exibições
- Última mensagem por menino de ouro

Qua Jan 30, 2013 01:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais Impróprias
por menino de ouro » Qui Jan 31, 2013 14:04
- 1 Respostas
- 1270 Exibições
- Última mensagem por e8group

Qui Jan 31, 2013 16:42
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integrais Impróprias
por dehcalegari » Qua Out 02, 2013 18:43
- 3 Respostas
- 1809 Exibições
- Última mensagem por dehcalegari

Seg Out 21, 2013 16:36
Cálculo: Limites, Derivadas e Integrais
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8828 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
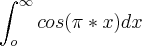 é divergente?
é divergente? (com limite superior b e inferior zero, para calcular a integral definida), mas não intendi porque ela diverge.
(com limite superior b e inferior zero, para calcular a integral definida), mas não intendi porque ela diverge.
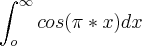 é divergente?
é divergente? (com limite superior b e inferior zero, para calcular a integral definida), mas não intendi porque ela diverge.
(com limite superior b e inferior zero, para calcular a integral definida), mas não intendi porque ela diverge.
 , então nas diversas formas de
, então nas diversas formas de  ir para
ir para  , estes limites tbm valeriam
, estes limites tbm valeriam  .
. 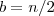 com
com  natural .
natural .  .
. 


 .
.



