
É um exercício do livro do James Stewart. A resposta é -4
poderiam me ajudar?
Obrigada



 é raiz dos dois polinômios do numerador e denominador e também que
é raiz dos dois polinômios do numerador e denominador e também que  (multiplicidade 2) é raiz do denominador ; de fato :
(multiplicidade 2) é raiz do denominador ; de fato : 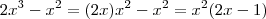 . Por definição de módulo , definida qualquer aplicação em que sua imagem é subconjunto dos reais , vale que
. Por definição de módulo , definida qualquer aplicação em que sua imagem é subconjunto dos reais , vale que 
 para todo x , basta então verificar quando
para todo x , basta então verificar quando  é positivo,nulo ou negativo e assim usar a expressão correspondente que condiz com intervalo que você está trabalhando .
é positivo,nulo ou negativo e assim usar a expressão correspondente que condiz com intervalo que você está trabalhando .  ,mas muito muito próximos dos mesmo . Isto é , dado
,mas muito muito próximos dos mesmo . Isto é , dado  suficientemente pequeno o quanto você queira , o que acontece com
suficientemente pequeno o quanto você queira , o que acontece com  com
com  ? Será que
? Será que  se aproxima de um número real
se aproxima de um número real  ,de modo que exista
,de modo que exista  pequeno (demais !) para qual o erro cometido na aproximação de
pequeno (demais !) para qual o erro cometido na aproximação de  por
por  seja sempre menor que
seja sempre menor que  ?
?  para x em um intervalo (a princípio desconhecido ) , vc então resolve formalizar está intuição e propõe um
para x em um intervalo (a princípio desconhecido ) , vc então resolve formalizar está intuição e propõe um  qualquer , quanto menor ele ,mais próximos estaremos de L , certo ? Desde que x verifique isso . E para x verificar isto , vc tbm verifica e existência do
qualquer , quanto menor ele ,mais próximos estaremos de L , certo ? Desde que x verifique isso . E para x verificar isto , vc tbm verifica e existência do  pequeno (mt mesmo !) dependendo do
pequeno (mt mesmo !) dependendo do  para o qual f(x) se aproxima de L com erro sempre menor que
para o qual f(x) se aproxima de L com erro sempre menor que  sempre que x está em (0.5 -\delta ,0.5) .
sempre que x está em (0.5 -\delta ,0.5) . 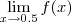 é estudar f(x) na vizinhança de 0.5 (o ponto 0.5 não importa ! E sim , seus "vizinhos" ) .
é estudar f(x) na vizinhança de 0.5 (o ponto 0.5 não importa ! E sim , seus "vizinhos" ) . 
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



