 por Flawyo » Qua Mai 21, 2014 14:54
por Flawyo » Qua Mai 21, 2014 14:54
Olá Santhiago,
Eu na verdade ainda tenho medo da própria matemática. Eu não tive uma boa história com meus professores de matemática.
Nos meus últimos dias de aula do 3º ano do Ensino Médio, por acaso eu acabei contando a um colega que meu sonho era estudar na USP. Esse colega contou para todos os outros, até que isso chegou ao ouvido do professor de Matemática. Estávamos na aula dele. E, ele era um dos padrinhos da nossa turma. Logo que este professor ficou sabendo, ele gritou para todos: "Então o fulano quer estudar em uma das melhores Universidades do país?". Ao dizer isso, ele começou a rir... Ele ria sem parar, e logo todos estavam rindo de mim e do meu sonho. Eu respirei fundo, porque não queria chorar na frente deles... Eu então, levantei do meu lugar e fui até a frente da sala e diante dele eu disse gaguejando: "Você ri de mim e esqueci que ri de você mesmo... Afinal, quem foi meu professor de matemática desde a Oitava Série até hoje?". Obviamente, ele parou de rir, mas respondeu dizendo que eu já estava reprovado na disciplina dele. E estaria mesmo, se a Diretora da Escola não fosse madrinha da nossa turma e tivesse entrado no meio desta história.
Minha vida se resume ao fracasso escolar nas disciplinas relacionadas a exatas. E depois desta última experiência, eu chorei durante vários dias, porque eu sabia que por mais que meu Professor tivesse cometido um erro, ele tinha razão, eu não tinha conhecimento suficiente de exatas para disputar uma vaga na USP. E o pior eu achava que eu era culpado por isso. Achava que eu tinha algum problema mental ou neurológico. E desisti da USP, desisti de medicina, porque achava que não daria conta.
Fui me dedicar ao que muito sabia, eu era bom entendedor da filosofia, da biologia, da poesia. Desde cedo eu ganhei concursos de redação. Logo, me decidi pela psicologia, um curso relacionado com o que eu gostava e nada de matemática, pensava eu. Para meu espanto, no primeiro semestre eu me deparei com a estatística aplicada à psicologia e sem saber nada de matemática eu só queria fazer pesquisas tendo como arcabouço a estatística, eu ficava fascinado com números e cálculos. Supri minha deficiência aprendendo a teoria e usando programas para os cálculos. A pesquisa que resultou no meu TCC foi baseada inteiramente na estatística, em cálculos de significância.
Então, a psicologia me confrontou várias vezes com esse medo dos números e a paixão pelas letras. Me lembrei da medicina que tinha abandonado.
Um dia eu decidi ir atrás do por que eu não tinha aprendido matemática. Fui em neurologista, psicopedagogo, pedagogo etc. Ninguém soube responder. Eu era normal! Tomografia do cérebro sem lesões, não havia presença de discalculia, nada.
Sem saber para quem ou para onde ir, para resolver isso, andando no centro da minha cidade e pensando no que fazer eu me deparei com o Kumon. Mesmo desconfiado de que eu poderia não aprender nada lá, afinal, nunca tinha aprendido nada além de contar ou operar cálculos simples, eu aceitei o desafio. E entrei.
Em 2 anos eu já sabia muito mais de matemática, do que em 13 anos de vida escolar. E agora com 3 anos (isso, porque eu fique alguns meses doente) eu estou concluindo o Kumon, sabendo infinitamente mais. Não há como comparar.
Mais os fantasmas estão todos por aqui ainda. Tem dias que eu não acredito no que sei. O pessoal do Kumon diz que isso é claramente uma limitação para mim.
Enfim, minha modéstia, tem muitos significados.
Eu concordo com você sobre a beleza dos símbolos na matemática. Mas, se às vezes eu tenho medo dos números, imagina os símbolos (risos). Eu, entendo boa parte deles, mas meus bloqueios às vezes me impedem de ir adiante.
Você falando do seu encantamento com Leibniz, eu me lembrei do meu deslumbramento com Euler ao propor seus números e a fórmula da identidade. Eu não entendo aquela fórmula, mas fiquei fascinado nela e ela me motiva a continuar com a matemática, assim, como os estudos de Agnesi. Como aquela mulher conseguiu pegar os estudos de Newton e Leibniz e entendê-los a tal ponto de simplificá-los é de tirar o chapéu.
Por fim, pois, já me prolonguei demais. O infinito é algo realmente impressionante, afinal, onde quer que olhemos lá está ele, especialmente na natureza.
Então, só posso dizer a você que mesmo com os contratempos que mencionei, a matemática é sim apaixonante, principalmente porque ela é abstrata tal como as letras antes de formar uma palavra. E atualmente, penso numa forma de integrar a matemática, a psicologia e a medicina. Eu acho que encontrei, num antigo projeto que escrevi a respeito da nanotecnologia.
Uma ótima semana para você!


 , concluímos que
, concluímos que 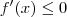 sempre que
sempre que ![x \in [-1,1] x \in [-1,1]](/latexrender/pictures/8800171bb0fc3d3e5b8f54c0ebda5095.png) ( o que significa que a função f é decrescente(= monótona não-crescente) [def . vide :
( o que significa que a função f é decrescente(= monótona não-crescente) [def . vide :  sempre que
sempre que 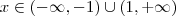 ( o que significa que a função f é estritamente crescente [def . vide :
( o que significa que a função f é estritamente crescente [def . vide : 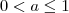 , segue
, segue ![[-a,a] \subset [-1,1] [-a,a] \subset [-1,1]](/latexrender/pictures/bf7c63440c476c50036eb82295725dd8.png) . De (a) , resulta que
. De (a) , resulta que ![max\{f(x); x \in [-a,a] \} = f(-a) = -a^3 +3a max\{f(x); x \in [-a,a] \} = f(-a) = -a^3 +3a](/latexrender/pictures/4f9a19f7bcb43e32863c5159bac1447f.png) .
. 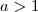 . Podemos reescrever o intervalo
. Podemos reescrever o intervalo ![[-a,a] [-a,a]](/latexrender/pictures/188b8d2ccb3b1d52985a3a3e5cf71fdb.png) como
como ![[-a,-1] \cup[-1,1] \cup (1,a] [-a,-1] \cup[-1,1] \cup (1,a]](/latexrender/pictures/a19d797f6853f4e3e2342799f5620da8.png) .
. ![[-a,-1] \subset (-\infty,-1] [-a,-1] \subset (-\infty,-1]](/latexrender/pictures/c61f8aad59601997e4fa539e71ece59f.png) . (Neste intervalo a função não é estritamente crescente , mas é crescente ) . Segue
. (Neste intervalo a função não é estritamente crescente , mas é crescente ) . Segue ![max\{f(x); x \in [-a,-1] \} = f(-1) max\{f(x); x \in [-a,-1] \} = f(-1)](/latexrender/pictures/cfed5d44da918076a1990e5a7e29326c.png) .
. ![(1,a] \subset (1,+\infty) (1,a] \subset (1,+\infty)](/latexrender/pictures/cfe2af715c194fc05d2979bf1ea69b94.png) então de (b) resulta
então de (b) resulta ![max \{f(x); x \in (1,a] \} = f(a) = a^3 -3a max \{f(x); x \in (1,a] \} = f(a) = a^3 -3a](/latexrender/pictures/ebb57dae95264d2bc207b445e0652ab8.png) .
. 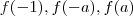 ? Vamos determinar
? Vamos determinar ![max\{f(-1) , f(-a), f(a) \} = max\{f(x); x \in [-a,a] \} max\{f(-1) , f(-a), f(a) \} = max\{f(x); x \in [-a,a] \}](/latexrender/pictures/0894417d4ccdb26d434ad784ce1fc6eb.png) .
. 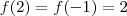 , como
, como  é crescente em
é crescente em ![(1,2] (1,2]](/latexrender/pictures/82a2d3646998b80552965f9919d183c5.png) resulta que
resulta que ![2 \geq f(x) , \forall x \in (1,2] 2 \geq f(x) , \forall x \in (1,2]](/latexrender/pictures/64073c50fdee2c9b4b0acb409d3b7823.png) .
. 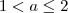 então
então ![max\{ f(a) ,f(-a) ,f(-1) \} = max\{f(x); x \in [-a,a] \} = f(-1) = 2 max\{ f(a) ,f(-a) ,f(-1) \} = max\{f(x); x \in [-a,a] \} = f(-1) = 2](/latexrender/pictures/25fc666ea60c080660d842699ea48fc8.png)
 , então ,
, então , ![max\{f(-1) , f(-a), f(a) \} = max\{f(x); x \in [-a,a] \} = f(a)= a^3 -3a max\{f(-1) , f(-a), f(a) \} = max\{f(x); x \in [-a,a] \} = f(a)= a^3 -3a](/latexrender/pictures/a72bf3bf31f5decda587fab2e43b0f1f.png)

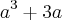 o valor de "a" ficará negativo, e como a>0, então não poderia ser F(2). Já quando substituímos F(1) que se transforma em F(-1), pois substituindo 1 em F(-a) realmente o "a" fica positivo.
o valor de "a" ficará negativo, e como a>0, então não poderia ser F(2). Já quando substituímos F(1) que se transforma em F(-1), pois substituindo 1 em F(-a) realmente o "a" fica positivo.![[-a,-1] \cup [-1,1] \cup (1,a] [-a,-1] \cup [-1,1] \cup (1,a]](/latexrender/pictures/11e226c955b33473e241a6b38d20bcbc.png) . Por que fazer isso ? Justificativa está em (a) e (b) .
. Por que fazer isso ? Justificativa está em (a) e (b) .  fixo em
fixo em ![f([-a,a]) = \{f(x) ; x \in [-a,a]\} f([-a,a]) = \{f(x) ; x \in [-a,a]\}](/latexrender/pictures/e47b44ab6946cb2c7b89093d68751e90.png) e o maior número deste conjunto é denotado por
e o maior número deste conjunto é denotado por ![max f([-a,a]) = max\{f(x) ; x \in [-a,a\} max f([-a,a]) = max\{f(x) ; x \in [-a,a\}](/latexrender/pictures/e5d0dd1b9e26a439503e899d62a958a0.png) )
) 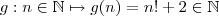 .
. 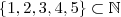 e
e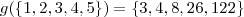 .
.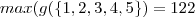 e
e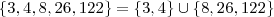
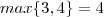 e
e 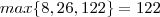 resulta
resulta 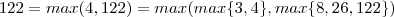 .
. 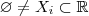 possui máximo , digamos,
possui máximo , digamos, 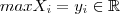 para
para 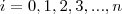 , então
, então 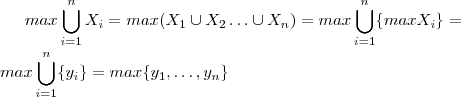
![f([-a,a]) = f([-a,-1]) \cup f([-1,-1]) \cup f((1,a]) f([-a,a]) = f([-a,-1]) \cup f([-1,-1]) \cup f((1,a])](/latexrender/pictures/70249d8d516c623b2181238a708d4c3d.png) . Então ,
. Então , ![max(f([-a,a])) = max \{ max f([-a,-1]) , max f([-1,-1]) , max f((1,a]) \} max(f([-a,a])) = max \{ max f([-a,-1]) , max f([-1,-1]) , max f((1,a]) \}](/latexrender/pictures/4c843292bb784bd2a20f566cf2b061fd.png) . Usando (a) e (b) concluímos que
. Usando (a) e (b) concluímos que ![max f([-a,-1]) = f(-a) max f([-a,-1]) = f(-a)](/latexrender/pictures/0e1df04f714a0f7a56e6c727759203f7.png) ,
,![max f([-1,-1]) = f(-1) max f([-1,-1]) = f(-1)](/latexrender/pictures/94654bd0dd5a1ea89d8603a2aa3fa1fd.png) e
e ![max f((1,a]) = f(a) max f((1,a]) = f(a)](/latexrender/pictures/ce3e6d01b60b2d4113d924413240a1db.png) .
. ![max f([-a,a]) = max \{f(-a) , f(-1) , f(a) \} max f([-a,a]) = max \{f(-a) , f(-1) , f(a) \}](/latexrender/pictures/8df2e40bca33bb495ba5aac450e54aba.png) .
.  , nos temos que os números
, nos temos que os números 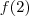 e
e  são iguais e
são iguais e 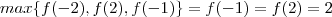 . Agora se
. Agora se 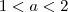 ,
, 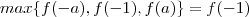 . Ao invés de uma condição a mais que é desnecessária , podemos simplesmente dizer que para
. Ao invés de uma condição a mais que é desnecessária , podemos simplesmente dizer que para 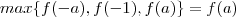 , pois ,
, pois , 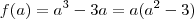 , mas
, mas 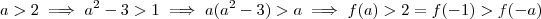 .
. 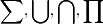 e etc , são muito uteis , o primeiro por exemplo para compactar somas , o segundo para união de vários conjuntos .E convenhamos , não sei se você pensa o mesmo , mas acho a matemática muita linda quando escrita nesta forma .
e etc , são muito uteis , o primeiro por exemplo para compactar somas , o segundo para união de vários conjuntos .E convenhamos , não sei se você pensa o mesmo , mas acho a matemática muita linda quando escrita nesta forma . em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.