Polinômios definidos em um intervalo aberto são sempre diferenciáveis .
Considere

e

.
Como ambos polinômios estão definidos em intervalos abertos , logo eles são diferenciáveis .Assim , usando que diferenciabilidade implica continuidade já podemos afirmar que a função

é contínua em

.Agora vamos mostrar que

é diferenciável em x = 1 e com isso concluir que f é contínua .
Por definição ,
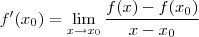
desde que o limite exista . E quando o limite existe ? Quando os limites laterais de f são números reais e são iguais .
Assim ,
(i)

.Como estamos trabalhando com

então

.Segue
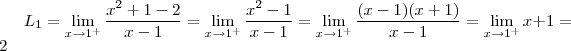
.
(ii)


é diferenciável em x = 1 .Só por curiosidade f é diferenciável em toda reta .
OBS.: Só para efeito de organização (vide regras do fórum ) evite postar mais de uma dúvida em um único tópico , uma dúvida para cada tópico . Além disso , anexe imagens somente se for necessário . Neste caso pode usar o LaTeX para digitar suas expressões .





 e
e  .
. é contínua em
é contínua em  .Agora vamos mostrar que
.Agora vamos mostrar que 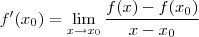 desde que o limite exista . E quando o limite existe ? Quando os limites laterais de f são números reais e são iguais .
desde que o limite exista . E quando o limite existe ? Quando os limites laterais de f são números reais e são iguais .  .Como estamos trabalhando com
.Como estamos trabalhando com  então
então  .Segue
.Segue 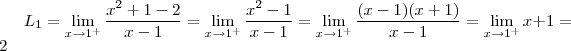 .
.
 é diferenciável em x = 1 .Só por curiosidade f é diferenciável em toda reta .
é diferenciável em x = 1 .Só por curiosidade f é diferenciável em toda reta . 
