-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480052 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 538193 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 501991 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 723585 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2157904 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por rodrigo lara » Sáb Jan 04, 2014 17:53
por rodrigo lara » Sáb Jan 04, 2014 17:53
Um ponto P move-se ao longo da elipse x² + 4y² = 1 . A abscissa x está variando a uma velocidade dx/dt = sen(4t). Mostre que;
A) dy/dt = - x.sen(4t) / 4y
B) d²y/dt² = sen²(4t) + 16xy²cos(4t) / 16y³
-
rodrigo lara
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Dez 27, 2013 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por e8group » Dom Jan 05, 2014 16:21
por e8group » Dom Jan 05, 2014 16:21
O que você tentou ?
No item (a) basta derivar ambos lados da eq. elipse com respeito a

.(Atenção a regra da cadeia) . Em seguida isole
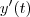
.No item(b) é suficiente derivar a expressão correspondente a
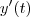
para provar este item .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rodrigo lara » Ter Jan 07, 2014 21:21
por rodrigo lara » Ter Jan 07, 2014 21:21
Sim. Fiz a derivada implicita em relação a t, somente o item A esta dando certo, ja o item B não esta batendo o resultado, poderia fazer pra mim compreender onde estou errando?
-
rodrigo lara
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Dez 27, 2013 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por e8group » Ter Jan 07, 2014 22:49
por e8group » Ter Jan 07, 2014 22:49
OK. Aceitando que (a) é verdadeiro ,sua derivada(com respeito a t) nos dá
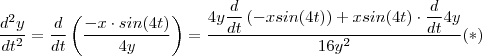
(regra do quociente) . Usando que
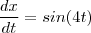
e o item (a) ,temos :

e daí
![4y \dfrac{d}{dt} \left(-xsin(4t) \right) + x sin(4t) \cdot \dfrac{d}{dt} 4y = -4y( sin^2(4t) + 4x cos(4t)) + 4 xsin(4t) \frac{-x \cdot sin(4t)}{4y} = \frac{-4y^2(sin^2(4t) + 4xcos(4t) ) -x^2 sin^2(4t)}{y} =\frac{-sin^2(4t)[x^2 + 4y^2] -16y^2 xcos(4t)}{y} = - \boxed{\frac{sin^2(4t) + 16y^2xcos(4t)}{y}} 4y \dfrac{d}{dt} \left(-xsin(4t) \right) + x sin(4t) \cdot \dfrac{d}{dt} 4y = -4y( sin^2(4t) + 4x cos(4t)) + 4 xsin(4t) \frac{-x \cdot sin(4t)}{4y} = \frac{-4y^2(sin^2(4t) + 4xcos(4t) ) -x^2 sin^2(4t)}{y} =\frac{-sin^2(4t)[x^2 + 4y^2] -16y^2 xcos(4t)}{y} = - \boxed{\frac{sin^2(4t) + 16y^2xcos(4t)}{y}}](/latexrender/pictures/2f999ce20e9d2ab1c8b9444dbea9a0eb.png)
.Quando substituirmos a expressão destacada em

o resultado segue .
Comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por rodrigo lara » Qua Jan 08, 2014 12:39
por rodrigo lara » Qua Jan 08, 2014 12:39
No item B o quociente é 16 y³ como vou chegar nisso. não entendi como aparece esse termo.
-
rodrigo lara
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Dez 27, 2013 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por rodrigo lara » Qua Jan 08, 2014 13:01
por rodrigo lara » Qua Jan 08, 2014 13:01
Se puder continuar, porque ficou meio confuso e não consegui entender direito, obrigado.
-
rodrigo lara
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Dez 27, 2013 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função implícita]mera coincidência no resultado?
por marcosmuscul » Qua Abr 03, 2013 20:30
- 1 Respostas
- 1236 Exibições
- Última mensagem por Russman

Qua Abr 03, 2013 22:25
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Implícita
por ariclenesmelo » Ter Out 23, 2012 14:32
- 3 Respostas
- 2517 Exibições
- Última mensagem por young_jedi

Qui Out 25, 2012 22:33
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Implicita
por Janoca » Dom Jun 22, 2014 02:40
- 3 Respostas
- 6240 Exibições
- Última mensagem por jugrigori

Dom Jun 03, 2018 16:05
Cálculo: Limites, Derivadas e Integrais
-
- [derivada implícita]exercício
por luiz_henriquear » Seg Out 24, 2011 20:48
- 5 Respostas
- 3645 Exibições
- Última mensagem por LuizAquino

Ter Nov 01, 2011 23:04
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Função Implicita
por fabriel » Sex Mar 15, 2013 13:27
- 1 Respostas
- 1293 Exibições
- Última mensagem por e8group

Sex Mar 15, 2013 21:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 29 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .(Atenção a regra da cadeia) . Em seguida isole
.(Atenção a regra da cadeia) . Em seguida isole 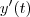 .No item(b) é suficiente derivar a expressão correspondente a
.No item(b) é suficiente derivar a expressão correspondente a 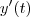 para provar este item .
para provar este item .

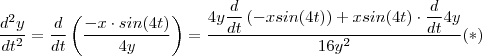 (regra do quociente) . Usando que
(regra do quociente) . Usando que 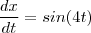 e o item (a) ,temos :
e o item (a) ,temos : e daí
e daí ![4y \dfrac{d}{dt} \left(-xsin(4t) \right) + x sin(4t) \cdot \dfrac{d}{dt} 4y = -4y( sin^2(4t) + 4x cos(4t)) + 4 xsin(4t) \frac{-x \cdot sin(4t)}{4y} = \frac{-4y^2(sin^2(4t) + 4xcos(4t) ) -x^2 sin^2(4t)}{y} =\frac{-sin^2(4t)[x^2 + 4y^2] -16y^2 xcos(4t)}{y} = - \boxed{\frac{sin^2(4t) + 16y^2xcos(4t)}{y}} 4y \dfrac{d}{dt} \left(-xsin(4t) \right) + x sin(4t) \cdot \dfrac{d}{dt} 4y = -4y( sin^2(4t) + 4x cos(4t)) + 4 xsin(4t) \frac{-x \cdot sin(4t)}{4y} = \frac{-4y^2(sin^2(4t) + 4xcos(4t) ) -x^2 sin^2(4t)}{y} =\frac{-sin^2(4t)[x^2 + 4y^2] -16y^2 xcos(4t)}{y} = - \boxed{\frac{sin^2(4t) + 16y^2xcos(4t)}{y}}](/latexrender/pictures/2f999ce20e9d2ab1c8b9444dbea9a0eb.png) .Quando substituirmos a expressão destacada em
.Quando substituirmos a expressão destacada em  o resultado segue .
o resultado segue . 


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.