 por ronaldo9nine » Qua Nov 20, 2013 10:31
por ronaldo9nine » Qua Nov 20, 2013 10:31
Olá, gostaria de saber como é feita a dedução da formula do volume do cone por meio de revolução( por integral)
abs.
-
ronaldo9nine
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Nov 20, 2013 10:27
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qua Nov 20, 2013 20:06
por e8group » Qua Nov 20, 2013 20:06
Há uma demonstração aqui
http://en.wikipedia.org/wiki/Cone . Também é possível por soma de Riemann ,veja
Considere o seguimento de reta
![y = \frac{r}{h} \cdot x , x \in [0,h] y = \frac{r}{h} \cdot x , x \in [0,h]](/latexrender/pictures/9495b653b3d477281913cc63722cda98.png)
(r,h > 0) . Girando este segmento em torno do eixo x iremos obter o cone circular de raio

e altura

.Dividindo

em n partes iguais e denotando
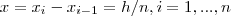
onde
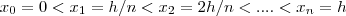
.
No intervalo
![I_{i}= [x_{i-1},x_i]
,n I_{i}= [x_{i-1},x_i]
,n](/latexrender/pictures/e1bd29a0b9896b1ae0dd52e9ac263ff9.png)
, a interseção do plano
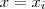
com o cone será um circulo cuja área é constante e é igual a
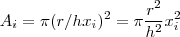
. Assim o volume de cada fatia é
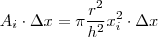
e portanto o volume do cone pode ser aproximado por
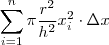
. Passando ao limite com
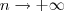
, obtemos a fórmula

.
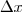
vira "dx" ,
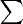
vira
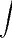
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [volume do cubo] Soma dos volumes das infinitas caixas
 por Priscilamoraes307 » Sex Ago 10, 2012 23:14
por Priscilamoraes307 » Sex Ago 10, 2012 23:14
- 2 Respostas
- 2196 Exibições
- Última mensagem por Russman

Sáb Ago 11, 2012 16:08
Geometria Espacial
-
- [Volumes de sólidos por rotação] Volume mudando os eixos
por Edmond Dantes » Sáb Out 20, 2018 11:31
- 2 Respostas
- 5868 Exibições
- Última mensagem por Edmond Dantes

Sáb Out 20, 2018 16:40
Cálculo: Limites, Derivadas e Integrais
-
- [volume] Cone
 por plugpc » Qui Jul 10, 2008 19:15
por plugpc » Qui Jul 10, 2008 19:15
- 3 Respostas
- 5330 Exibições
- Última mensagem por admin

Sex Jul 11, 2008 03:42
Geometria Espacial
-
- VOLUME DO CONE
por EULER » Sáb Jul 31, 2010 22:59
- 2 Respostas
- 4027 Exibições
- Última mensagem por EULER

Ter Ago 03, 2010 14:08
Geometria Espacial
-
- Volume do Cone
por garciarafael » Seg Jul 18, 2011 22:00
- 3 Respostas
- 2922 Exibições
- Última mensagem por garciarafael

Seg Jul 18, 2011 23:52
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![y = \frac{r}{h} \cdot x , x \in [0,h] y = \frac{r}{h} \cdot x , x \in [0,h]](/latexrender/pictures/9495b653b3d477281913cc63722cda98.png) (r,h > 0) . Girando este segmento em torno do eixo x iremos obter o cone circular de raio
(r,h > 0) . Girando este segmento em torno do eixo x iremos obter o cone circular de raio  e altura
e altura  .Dividindo
.Dividindo  em n partes iguais e denotando
em n partes iguais e denotando 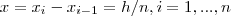 onde
onde 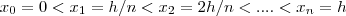 .
. ![I_{i}= [x_{i-1},x_i]
,n I_{i}= [x_{i-1},x_i]
,n](/latexrender/pictures/e1bd29a0b9896b1ae0dd52e9ac263ff9.png) , a interseção do plano
, a interseção do plano 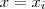 com o cone será um circulo cuja área é constante e é igual a
com o cone será um circulo cuja área é constante e é igual a 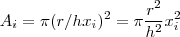 . Assim o volume de cada fatia é
. Assim o volume de cada fatia é 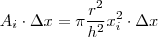 e portanto o volume do cone pode ser aproximado por
e portanto o volume do cone pode ser aproximado por 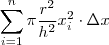 . Passando ao limite com
. Passando ao limite com 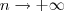 , obtemos a fórmula
, obtemos a fórmula  .
.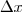 vira "dx" ,
vira "dx" , 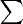 vira
vira 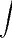 .
.