que contem um capacitor com capacitância de C Farads (F); um resistor
com uma resistência de R ohms (
 ); com carga Q medida em coulombs; voltagem E(t)
); com carga Q medida em coulombs; voltagem E(t) medida em volts e o tempo t medido em segundos.
Supondo que , R=2
 , C=0,01 F, Q(0)=0 e E(t)=10sen (60t), calcule a carga e a corrente i
, C=0,01 F, Q(0)=0 e E(t)=10sen (60t), calcule a carga e a corrente i no instante t. (observação a corrente i é dada por i = dQ/dt ).
Me ajudem por favor é urgente preciso enviar a prova até dia 27/08 terça feira.




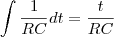

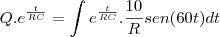
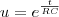



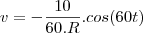



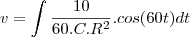
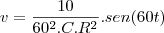
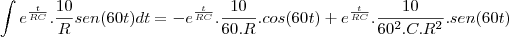






![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)