 por Josi » Ter Nov 03, 2009 17:30
por Josi » Ter Nov 03, 2009 17:30
Tenho um trabalho com a questão abaixo:
* Um fio de 12 cm pode ser curvado formando um círculo, dobrado formando um quadrado ou cortado em duas partes fazendo um círculo e um quadrado. Quanto do fio deve ser usado para o círculo para que a área total englobada pela(s) figura(s) seja:
a) máxima?
b) mínima?
Já tentei resolver de várias formas, mas os resultados estão sem lógica, como área negativa, comprimento maior que 12, entre outros... Não sou muito boa com fórmulas geométricas, então se alguém puder me ajudar fico muito grata...
-
Josi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Set 10, 2009 16:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por marciommuniz » Ter Nov 03, 2009 22:30
por marciommuniz » Ter Nov 03, 2009 22:30
Olá, procure sobre Máximos e Mínimos de funções.
Basta aplicar primeira e segunda derivada. Deixe aqui seus cálculos, se tiver ainda dúvidas, reposte.
Lembrando que a área do círculo é
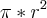
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicações de Derivada - Problemas de Otimização - Socorro!!
por Josi » Ter Nov 03, 2009 17:31
- 1 Respostas
- 4757 Exibições
- Última mensagem por Elcioschin

Qua Nov 04, 2009 08:40
Cálculo: Limites, Derivadas e Integrais
-
- Problemas de Otimização
por lucasabreuo » Seg Mai 06, 2019 11:52
- 0 Respostas
- 2196 Exibições
- Última mensagem por lucasabreuo

Seg Mai 06, 2019 11:52
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda com problemas de otimização
por sergioluizom » Ter Abr 17, 2012 16:15
- 1 Respostas
- 9417 Exibições
- Última mensagem por LuizAquino

Sex Abr 20, 2012 19:10
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações da Derivada
por Bruhh » Qua Jun 02, 2010 19:00
- 2 Respostas
- 4780 Exibições
- Última mensagem por Bruhh

Sáb Jun 05, 2010 18:25
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações da Derivada
por Thyago Quimica » Seg Out 29, 2012 18:44
- 1 Respostas
- 2870 Exibições
- Última mensagem por e8group

Seg Out 29, 2012 19:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


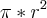

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
