lim (2^x - 3^x), quando x->

lim ((1 - 2^x)/(1 - 3^x)), quando x->

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Como tentei resolver:
lim (2^x - 3^x), quando x->
 = lim (2^x), quando x->
= lim (2^x), quando x-> , - lim (3^x), quando x->
, - lim (3^x), quando x-> =
=  -
-
(Mas este resultado é uma indeterminação. Tentei também de outras maneiras, mas todas sempre chegavam numa indeterminação).
lim ((1 - 2^x)/(1 - 3^x)), quando x->
 = lim (1 - 2^x),quando x->
= lim (1 - 2^x),quando x-> / lim (1 - 3^x), quando x->
/ lim (1 - 3^x), quando x->
(indeterminação).


 se aproxima de infinito mais rapidamente que
se aproxima de infinito mais rapidamente que 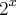 , pois
, pois  . Assim, o primeiro limite vai para
. Assim, o primeiro limite vai para  .
. . A estratégia é tentar reescrevê-lo de tal modo que não haja mais indeterminação. Para isso, note que colocando
. A estratégia é tentar reescrevê-lo de tal modo que não haja mais indeterminação. Para isso, note que colocando  em evidência obtemos:
em evidência obtemos:![\lim_{x\to +\infty} 3^x\left[\left(\frac{2}{3}\right)^x - 1\right] = (+\infty)\cdot (0 - 1) = -\infty \lim_{x\to +\infty} 3^x\left[\left(\frac{2}{3}\right)^x - 1\right] = (+\infty)\cdot (0 - 1) = -\infty](/latexrender/pictures/a27ac0e1686c0171f437b9e3073528b0.png)
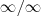 . Para remover esta indeterminação, note que dividindo o numerador e o denominador por
. Para remover esta indeterminação, note que dividindo o numerador e o denominador por 

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
