 por arthurvct » Qua Jul 10, 2013 16:48
por arthurvct » Qua Jul 10, 2013 16:48
1- Mostre que 2arcsen(x)-arccos(
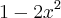
)=0. Para todo x tal que
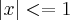
.
2-Determine os valores máximos e mínimos LOCAIS E ABSOLUTOS da função f(x)=
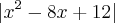
no intervalo [0, 5].
-
arthurvct
-
 por arthurvct » Qua Jul 10, 2013 16:51
por arthurvct » Qua Jul 10, 2013 16:51
faltou essa galera:
3-O raio de uma esfera é de 20cm. Estimar, através de diferenciais, o valor do volume com que fica a esfera ao aplicarmos uma camada de tinta de 0,1cm.
-
arthurvct
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão envolvendo Derivadas e área! Prova no sábado!!
por arthurvct » Qui Jun 13, 2013 15:21
- 1 Respostas
- 1622 Exibições
- Última mensagem por e8group

Sex Jun 14, 2013 00:49
Cálculo: Limites, Derivadas e Integrais
-
- urgente!! tenho prova amanhã!!
por hopiloto » Ter Jul 12, 2011 12:33
- 0 Respostas
- 1162 Exibições
- Última mensagem por hopiloto

Ter Jul 12, 2011 12:33
Sequências
-
- AJUDA, DÚVIDA EM 2 QUESTÕES E TENHO PROVA AMANHÃ
por ymath » Sáb Dez 11, 2010 03:16
- 2 Respostas
- 2778 Exibições
- Última mensagem por VtinxD

Dom Dez 12, 2010 18:39
Binômio de Newton
-
- duvida de uma prova AJUDEM
por lais_banestes » Qua Mai 16, 2012 21:45
- 0 Respostas
- 1159 Exibições
- Última mensagem por lais_banestes

Qua Mai 16, 2012 21:45
Estatística
-
- Prova de Aprendiz de Marinheiro Me ajudem por favor
por Talvane Ramos » Seg Mar 29, 2010 15:56
- 2 Respostas
- 1652 Exibições
- Última mensagem por Talvane Ramos

Seg Mar 29, 2010 16:15
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
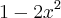 )=0. Para todo x tal que
)=0. Para todo x tal que 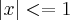 .
.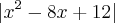 no intervalo [0, 5].
no intervalo [0, 5].
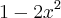 )=0. Para todo x tal que
)=0. Para todo x tal que 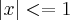 .
.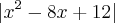 no intervalo [0, 5].
no intervalo [0, 5].
 .
.



