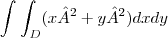 , onde D é a região do 1 quadrante limitada pelos hiperbóles:
, onde D é a região do 1 quadrante limitada pelos hiperbóles:[s]Obs:[/s] Ignore o A² , é apenas x²+y² , ainda não sei mexer nesse latex direito!!
x²-y² = 1
x²-y²=9
xy=2
xy=4
O que eu fiz até agora:
u = x²-y²
v = xy
Novos limites de integração:
Para u, de 1 a 9
Para v, de 2 a 4
Fiz o determinante matriz jacobiana J(u,v) = l Ux Vx l
l Uy Vy l
O determinante da Jacobiana (u,v) deu 2 ( x² + y² ) , logo, dudv = 2(x²+y²)dxdy => dxdy = dudv/(2(x²+y²))
Depois substitui na integral inicial, cortei os x²+y² , e ficou 1/2dxdv com os intervalos de integração que eu falei alí em cima.
Enfim, não esta conseguindo resolver nenhum exercício de integral dupla deste tipo, consegui esse, e fiquei na maior dúvida, isso tá certo ou fiz alguma besteira?



