 por Thyago Quimica » Dom Jun 16, 2013 16:38
por Thyago Quimica » Dom Jun 16, 2013 16:38
Boa Tarde pessoal resolvi um lista de exercícios de integrais, mais fiquei preso nessas...:
a)
![\int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx \int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx](/latexrender/pictures/796281c52df68bc6cc5c9fd2a904937a.png)
b)

c)
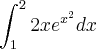
Desenvolvo todo o calculo mais o resultado não bate com o gabarito. Quem poder ajudar nem que seja com a saida agradeço muito.
Livro: Calculo I Guidorizzi
-
Thyago Quimica
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 05, 2012 17:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por e8group » Dom Jun 16, 2013 20:12
por e8group » Dom Jun 16, 2013 20:12
As integrais dos itens a) e b) possuem integrando na forma

com

racionais . Agora reescrevendo

como

temos

para
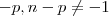
resulta

.A última integral , pode fazer a subsituição
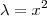
(porque ?) .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Teorema fundamental Calculo
por temujin » Seg Jun 17, 2013 17:36
- 1 Respostas
- 910 Exibições
- Última mensagem por temujin

Seg Jun 17, 2013 19:12
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo III] - Teorema de Stokes
por Feliperpr » Sáb Abr 21, 2012 16:08
- 5 Respostas
- 2630 Exibições
- Última mensagem por Feliperpr

Sáb Abr 21, 2012 19:33
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Calculo de limite usando o teorema do confronto.
por erickm93 » Qua Mai 22, 2013 10:48
- 3 Respostas
- 6024 Exibições
- Última mensagem por erickm93

Qua Mai 22, 2013 23:49
Cálculo: Limites, Derivadas e Integrais
-
- Calculo vetorial, integrais de linha e Teorema de green
 por Fernandobertolaccini » Qui Jun 11, 2015 20:19
por Fernandobertolaccini » Qui Jun 11, 2015 20:19
- 0 Respostas
- 2305 Exibições
- Última mensagem por Fernandobertolaccini

Qui Jun 11, 2015 20:19
Cálculo: Limites, Derivadas e Integrais
-
- Limite fundamental
por matmatco » Qui Set 01, 2011 11:04
- 6 Respostas
- 3468 Exibições
- Última mensagem por matmatco

Qui Set 08, 2011 10:19
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx \int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx](/latexrender/pictures/796281c52df68bc6cc5c9fd2a904937a.png)

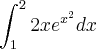

![\int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx \int_{1}^{4}\frac{1+x}{\sqrt[]{x}} dx](/latexrender/pictures/796281c52df68bc6cc5c9fd2a904937a.png)

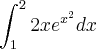

 com
com  racionais . Agora reescrevendo
racionais . Agora reescrevendo  como
como  temos
temos  para
para 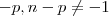 resulta
resulta  .A última integral , pode fazer a subsituição
.A última integral , pode fazer a subsituição 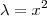 (porque ?) .
(porque ?) .