 , l > 0.
, l > 0.(a) Calcule a diferencial de A.
(b) Avalie o erro que se comete na aproximação de ?A por dA. Interprete geometricamente.
Na (a) eu fiz: A diferencial de A é dada por dA = A'dl e , portanto, dA = 2l dl.
na (b) eu fiz :?A
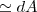 , então
, então f(l+dl) =
 + 2ldl+
+ 2ldl+ 
2ldl+
 = ?A
= ?AdA +
 = ?A
= ?Ae o erro é o

Está certo? como eu faço corretamente. E como interpreto geometricamente?


 é
é  .No outro exercício ,observando que
.No outro exercício ,observando que 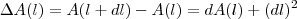 é o acréscimo que a função sofre ao passar de
é o acréscimo que a função sofre ao passar de  a
a  .Aproximando este valor por
.Aproximando este valor por 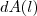 ,vemos que o erro
,vemos que o erro 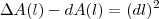 .
. 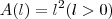 é uma função que nos fornece a área de um quadrado de lados
é uma função que nos fornece a área de um quadrado de lados 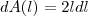 é um número aproximado para o acréscimo
é um número aproximado para o acréscimo 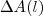 na área
na área 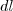 em
em 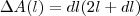 e
e  como áreas de dois retângulos de comprimentos
como áreas de dois retângulos de comprimentos  e
e 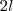 e alturas
e alturas 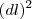 ;erro este que é a área de um quadrado de lados medindo
;erro este que é a área de um quadrado de lados medindo 
