por Sobreira » Qui Mai 16, 2013 01:20
Essa é uma questão de um concurso da petrobras.
Considere a função real de variável real , na qual x > 0 e ln(x) é o logaritmo neperiano de x.
A função derivada é
Indica como resposta:
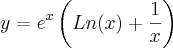
Apesar de eu achar que eh:
.
O que é correto?
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário
-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
por Sobreira » Qui Mai 16, 2013 08:54
Já verifiquei a resposta já.
É a derivada do produto.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário
-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- DERIVADA - CONCURSO PETROBRAS
por pinkfluor » Qua Mar 02, 2011 11:10
- 2 Respostas
- 2348 Exibições
- Última mensagem por LuizAquino
Qua Mar 02, 2011 12:06
Cálculo: Limites, Derivadas e Integrais
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:47
- 1 Respostas
- 3974 Exibições
- Última mensagem por LuizAquino
Ter Jan 24, 2012 21:12
Logaritmos
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:49
- 1 Respostas
- 1459 Exibições
- Última mensagem por LuizAquino
Ter Jan 24, 2012 21:51
Estatística
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:52
- 1 Respostas
- 3029 Exibições
- Última mensagem por LuizAquino
Ter Jan 24, 2012 22:08
Estatística
-
- Concurso Petrobras
por lourivallobo » Qua Jan 25, 2012 09:13
- 4 Respostas
- 3006 Exibições
- Última mensagem por Arkanus Darondra
Qua Jan 25, 2012 17:30
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 58 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
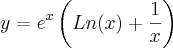
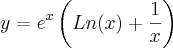
