-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477869 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529493 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493043 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 698974 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2109375 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por MarlonMO250 » Sex Mar 01, 2013 21:02
por MarlonMO250 » Sex Mar 01, 2013 21:02
Olá, tenho uma lista e estava resolvendo um exercicio usando a seguinte definição:

no caso são 3 questões no exercicio pra resolver com essa definição, uma delas eu consegui resolver, peço ajuda sómente pra saber se esta certo

a)

, e p=2


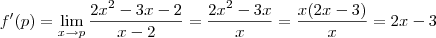
nessa questão eu to em duvida se esta certo por isso espero que me respondam

além dela também tem essa:
b)
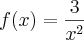
, e p=1
e essa
c)
![f(x)=\sqrt[3]{x} f(x)=\sqrt[3]{x}](/latexrender/pictures/415c4f39a1a68ccac15da99969baacfc.png)
, e p=8
ambas eu não consegui resolver, agradeço a atenção de todos

-
MarlonMO250
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Fev 03, 2013 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Sex Mar 01, 2013 21:25
por Russman » Sex Mar 01, 2013 21:25
A definição de derivada que você está usando NÃO está errada. Porém, se você tomar
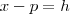
então teremos uma definição expressa de forma mais simples que, certamente o ajudará.
Veja que, fazendo isso, obtemos

.
Assim, se
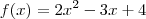
, então
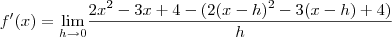
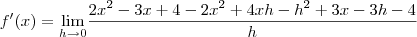
de onde, simplificando o que pode ser simplificado, obtemos

.
Efetuando a divisão por

o limite se torna
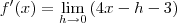
,
e , finalmente, tomando

:

Para

:
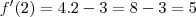
Tente usar essa definição alternativa para resolver os outros casos!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por felipeek » Sex Mar 01, 2013 22:00
por felipeek » Sex Mar 01, 2013 22:00
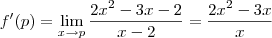
esse passo está errado! você não pode simplesmente 'cortar' os -2. O correto seria:
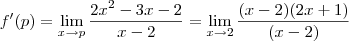
aí sim poderia cortar os (x-2)
abraços colega!
-
felipeek
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Mar 01, 2013 18:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por MarlonMO250 » Sex Mar 01, 2013 23:07
por MarlonMO250 » Sex Mar 01, 2013 23:07
russman, essa definição que você falou eu conheço, o problema é que a professora pediu na lista usando essa que eu falei

felipeek, no caso a derivada não ficaria 2x+1, sendo que é 4x-3

-
MarlonMO250
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Fev 03, 2013 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Sáb Mar 02, 2013 01:14
por Russman » Sáb Mar 02, 2013 01:14
Bom, se a tua professora insiste em ir pelo caminho mais difícil...e bem mais difícil, eu diria.

Substituindo a função, temos
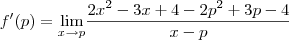
![f'(p) = \underset{x\rightarrow p }{\lim }\frac{2(x^2-p^2)-3(x-p)}{x-p} = \underset{x\rightarrow p }{\lim }\left [2\frac{(x^2-p^2)}{x-p}-\frac{3(x-p)}{(x-p)} \right ] f'(p) = \underset{x\rightarrow p }{\lim }\frac{2(x^2-p^2)-3(x-p)}{x-p} = \underset{x\rightarrow p }{\lim }\left [2\frac{(x^2-p^2)}{x-p}-\frac{3(x-p)}{(x-p)} \right ]](/latexrender/pictures/ccf4cbfa8f2535506e4b62e13f3d82e0.png)
de onde, simplificando e tomando
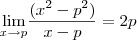
,

.
Note que , em

, basta você multiplicar o limite por

no numerador e no denominador que você o resolve.
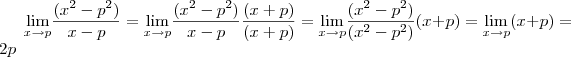
Eu acredito que essa definição induza o aluno a utilizar técnicas de resolução de limite que não lhe cabe para derivar uma simples função polinomial.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por felipeek » Sáb Mar 02, 2013 02:55
por felipeek » Sáb Mar 02, 2013 02:55
MarlonMO250 escreveu:russman, essa definição que você falou eu conheço, o problema é que a professora pediu na lista usando essa que eu falei

felipeek, no caso a derivada não ficaria 2x+1, sendo que é 4x-3

Você está fazendo confusão.
A derivada da função que você deu é sim 4x-3.
Note, entretanto, que você tentou resolver o exercício tomando
p=2. No momento que você faz isso, você substitui todas as variáveis
p da definição por 2 e
x que tendia a
p passa a tender a 2 (esse último você esqueceu de modificar ali no limite). O fato de você escolher um valor para a variável
p faz você obter como o resultado não uma Função Derivada geral (que seria 4x-3) e sim o RESULTADO da derivada no ponto que você escolheu (no caso p=2). Se você quisesse obter como resultado 4x-3, você deveria ter calculado o limite sem assumir um valor para
p. Aí sim, o resultado seria uma função derivada geral 4x-3 (no caso seria 4p-3) e aí sim você poderia substituir o x por 2 na função, obtendo a derivada no ponto x=2 que seria 5 (4*2-3 = 5).
O meu cálculo deu 2x+1 como resultado porque eu não terminei. Como
x tendia a
2, o passo final seria substiuir o
x por
2, obtendo como reposta final: 2(2)+1 = 5 . Ou seja, cinco é a derivada de x=2, ou ainda, 5 é a inclinação da reta tangente quando x=2. Obtemos direto o resultado de 5, sem obter a função derivada primeiro, pois assumimos direto p=2 no começo do exercicio (pensei que era assim que vc queria, pois foi vc mesmo que fez assim, na verdade, talvez seja isso mesmo que o exercicio quer)
-
felipeek
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Mar 01, 2013 18:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Sáb Mar 02, 2013 03:42
por Russman » Sáb Mar 02, 2013 03:42
Acredito que o amigo
felipeek tenha razão! Você tem de substituir imediatamente o valor de

no limite. Do contrário, como eu mostrei, você terá de utilizar técnicas de resolução de limite desnecessárias nessa etapa do conteúdo.
É bem verdade que, para
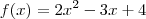
,

.
Veja que você está calculando a derivada de

com relação a

em um ponto específico , e não em um ponto genérico

. Para este, sim, teríamos

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Assíntotas, pontos de infexão e
por Laisa » Qua Fev 20, 2019 15:35
- 3 Respostas
- 10984 Exibições
- Última mensagem por rcompany

Qua Fev 20, 2019 20:09
Cálculo: Limites, Derivadas e Integrais
-
- [Pontos críticos - Derivadas] Ajuda com pontos críticos
por jonaskessinger » Qui Dez 13, 2012 18:16
- 1 Respostas
- 2952 Exibições
- Última mensagem por Russman

Qui Dez 13, 2012 19:35
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 1943 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 6816 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2448 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 28 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , e p=2
, e p=2

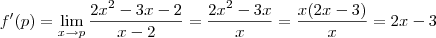

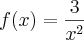 , e p=1
, e p=1![f(x)=\sqrt[3]{x} f(x)=\sqrt[3]{x}](/latexrender/pictures/415c4f39a1a68ccac15da99969baacfc.png) , e p=8
, e p=8


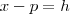 então teremos uma definição expressa de forma mais simples que, certamente o ajudará.
então teremos uma definição expressa de forma mais simples que, certamente o ajudará. .
.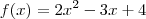 , então
, então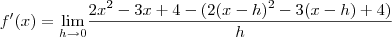
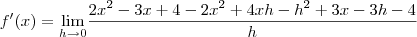
 .
. o limite se torna
o limite se torna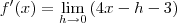 ,
, :
:
 :
: 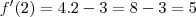

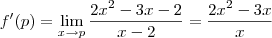
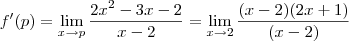



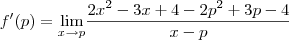
![f'(p) = \underset{x\rightarrow p }{\lim }\frac{2(x^2-p^2)-3(x-p)}{x-p} = \underset{x\rightarrow p }{\lim }\left [2\frac{(x^2-p^2)}{x-p}-\frac{3(x-p)}{(x-p)} \right ] f'(p) = \underset{x\rightarrow p }{\lim }\frac{2(x^2-p^2)-3(x-p)}{x-p} = \underset{x\rightarrow p }{\lim }\left [2\frac{(x^2-p^2)}{x-p}-\frac{3(x-p)}{(x-p)} \right ]](/latexrender/pictures/ccf4cbfa8f2535506e4b62e13f3d82e0.png)
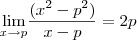 ,
, .
. , basta você multiplicar o limite por
, basta você multiplicar o limite por  no numerador e no denominador que você o resolve.
no numerador e no denominador que você o resolve.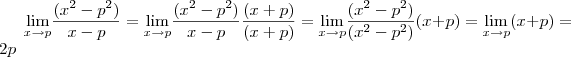
 no limite. Do contrário, como eu mostrei, você terá de utilizar técnicas de resolução de limite desnecessárias nessa etapa do conteúdo.
no limite. Do contrário, como eu mostrei, você terá de utilizar técnicas de resolução de limite desnecessárias nessa etapa do conteúdo. .
. com relação a
com relação a  em um ponto específico , e não em um ponto genérico
em um ponto específico , e não em um ponto genérico  .
.

 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo: