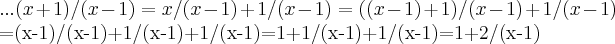-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478284 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532929 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496417 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 708943 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2127088 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Marlon Teofilo » Ter Jan 22, 2013 14:23
por Marlon Teofilo » Ter Jan 22, 2013 14:23
Oi boa tarde.
Estou com dificuldades em resolver um
limite.
é o seguinte:

entao, iniciei separando em duas frações, ambas com demoninador (x-1), fazendo os
limites separados.
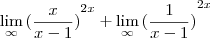
O segundo termo cheguei à conclusão que é 1/infinito=0
O primeiro termo conclui que a resposta do
limite é e^2, após mudar a base e todo aquele processo de sempre, hehehehe, gostaria de saber se está correto, pois desconfio que não! kkkkkkkk
-
Marlon Teofilo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jan 07, 2013 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por e8group » Ter Jan 22, 2013 17:43
por e8group » Ter Jan 22, 2013 17:43
Cuidado!
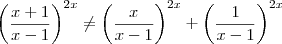
Como dica note que ,
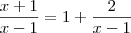
.
Logo ,
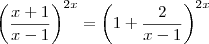
e portanto ,
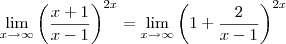
.
Além disso , tomando
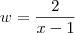
.Quando
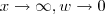
.Fazendo as substituições ,
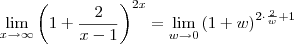
Usando as propriedades

e
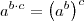
e também dos
limites, uma delas do produto .
Segue então :
![\lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4 \lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4](/latexrender/pictures/0e2d8979072ad1690fa73549a2250b33.png)
.
Obs.: Para compreender a resolução veja os
limites fundamentais em especial o
limite fundamental que denomina-se o número Euler . Para ler mais ,
http://pt.wikipedia.org/wiki/N%C3%BAmero_de_Euler .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Marlon Teofilo » Ter Jan 22, 2013 18:01
por Marlon Teofilo » Ter Jan 22, 2013 18:01
Obrigado, minha duvida realmente era se eu utilizei a propriedade de forma correta, e errei hehehehe
vlw mano, entendi!!!
-
Marlon Teofilo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jan 07, 2013 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por lyppeferreira_ » Sáb Abr 04, 2020 15:33
por lyppeferreira_ » Sáb Abr 04, 2020 15:33
e8group escreveu:Cuidado!
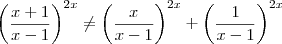
Como dica note que ,
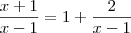
.
Logo ,
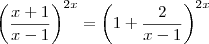
e portanto ,
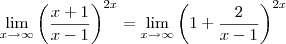
.
Além disso , tomando
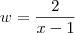
.Quando
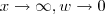
.Fazendo as substituições ,
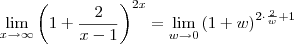
Usando as propriedades

e
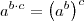
e também dos
limites, uma delas do produto .
Segue então :
![\lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4 \lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4](/latexrender/pictures/0e2d8979072ad1690fa73549a2250b33.png)
.
Obs.: Para compreender a resolução veja os
limites fundamentais em especial o
limite fundamental que denomina-se o número Euler . Para ler mais ,
http://pt.wikipedia.org/wiki/N%C3%BAmero_de_Euler .
Como você chegou nessa
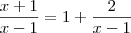
Tô travado nessa passagem. Eu tentei pela propriedade do quociente dos
limites, mas não cheguei nesse resultado que vc conseguiu.
-
lyppeferreira_
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 04, 2020 08:03
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por adauto martins » Dom Abr 05, 2020 11:20
por adauto martins » Dom Abr 05, 2020 11:20
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites de função exponencial
por Silas » Qui Jul 10, 2014 18:12
- 2 Respostas
- 1972 Exibições
- Última mensagem por Silas

Qui Jul 10, 2014 21:47
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Limite fundamental Exponencial
por antonelli2006 » Ter Set 20, 2011 05:54
- 1 Respostas
- 1821 Exibições
- Última mensagem por LuizAquino

Ter Set 20, 2011 12:22
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda sobre Limites seno e exponencial
por gn66 » Sex Jun 03, 2011 12:02
- 8 Respostas
- 4446 Exibições
- Última mensagem por gn66

Sex Jun 03, 2011 16:34
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 4463 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 3824 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 27 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

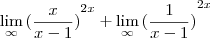


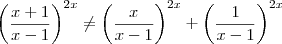
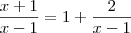 .
.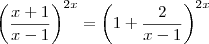
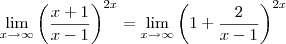 .
. 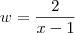 .Quando
.Quando 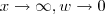 .Fazendo as substituições ,
.Fazendo as substituições , 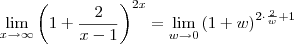
 e
e  e também dos
e também dos ![\lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4 \lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4](/latexrender/pictures/0e2d8979072ad1690fa73549a2250b33.png) .
.