 por rodrigonapoleao » Seg Jan 21, 2013 22:52
por rodrigonapoleao » Seg Jan 21, 2013 22:52
alguem me ajude a resolver este limite:
![\lim_{x\rightarrow0}\frac{{x}^{4}\sqrt[]{{sin}^{2}(x+1)}}{\sqrt[]{{x}^{4}+{x}^{2}}} \lim_{x\rightarrow0}\frac{{x}^{4}\sqrt[]{{sin}^{2}(x+1)}}{\sqrt[]{{x}^{4}+{x}^{2}}}](/latexrender/pictures/0aaf68532111bcf959b63ad1a0f2159c.png)
-
rodrigonapoleao
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Nov 19, 2012 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por e8group » Ter Jan 22, 2013 09:29
por e8group » Ter Jan 22, 2013 09:29
Note que ,
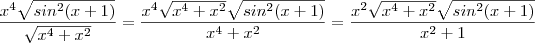
. Desta forma sairmos da indeterminação " 0/0 " .
Aplique a propriedade "limite do produto é o produto dos limites " e conclua que

tende a zero quando x se aproxima de zero .
Por favor ,tente expor suas tentativas na próxima vez que postar alguma dúvida .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4795 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5126 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7268 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow0}\frac{{x}^{4}\sqrt[]{{sin}^{2}(x+1)}}{\sqrt[]{{x}^{4}+{x}^{2}}} \lim_{x\rightarrow0}\frac{{x}^{4}\sqrt[]{{sin}^{2}(x+1)}}{\sqrt[]{{x}^{4}+{x}^{2}}}](/latexrender/pictures/0aaf68532111bcf959b63ad1a0f2159c.png)


![\lim_{x\rightarrow0}\frac{{x}^{4}\sqrt[]{{sin}^{2}(x+1)}}{\sqrt[]{{x}^{4}+{x}^{2}}} \lim_{x\rightarrow0}\frac{{x}^{4}\sqrt[]{{sin}^{2}(x+1)}}{\sqrt[]{{x}^{4}+{x}^{2}}}](/latexrender/pictures/0aaf68532111bcf959b63ad1a0f2159c.png)

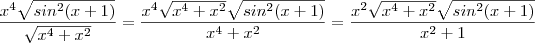 . Desta forma sairmos da indeterminação " 0/0 " .
. Desta forma sairmos da indeterminação " 0/0 " .  tende a zero quando x se aproxima de zero .
tende a zero quando x se aproxima de zero . 

 .
.
 :
: