 por thejotta » Dom Jan 13, 2013 23:56
por thejotta » Dom Jan 13, 2013 23:56
Determine uma função y=y(x) cujo gráfico passe pelo ponto (1,1) e tal que a reta tangente no ponto generico (x,y) tenha coeficiente angular
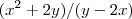
Alguém sabe como resolver essa questão não sei nem por onde começar.
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Seg Jan 14, 2013 03:14
por Russman » Seg Jan 14, 2013 03:14
Do enunciado partimos de
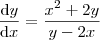
de modo que, reorganizando os termos, temos a seguinte forma:
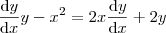
.
Note que o lado direito é exatamente a derivada do produto
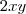
. Assim,
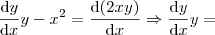
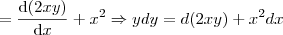
de forma que,
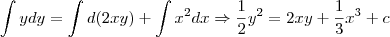
.
Agora faça

para calcular o valor da constante

e use o método de solução de equações de 2° grau para isolar

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por thejotta » Seg Jan 14, 2013 07:47
por thejotta » Seg Jan 14, 2013 07:47
Muito obrigado amigo
-
thejotta
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Seg Out 29, 2012 12:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10717 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9728 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3314 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4609 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6531 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
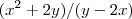

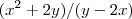

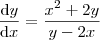
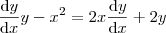 .
. 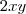 . Assim,
. Assim, 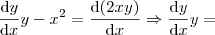
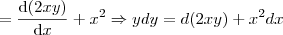
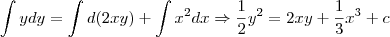 .
. para calcular o valor da constante
para calcular o valor da constante  e use o método de solução de equações de 2° grau para isolar
e use o método de solução de equações de 2° grau para isolar  .
.
