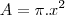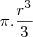por iarapassos » Ter Jan 08, 2013 14:48
por iarapassos » Ter Jan 08, 2013 14:48
Calculo o volume de um sólido que tem para base um circulo de raio r e cujas seções transversais a um diâmetro da mesma são triangulos retangulos isosceles, todos situados em um mesmo semi-espaço em relaçao ao plano que a contem, e quem têm como um dos seus catetos cordas da circunferencia da base, perpendiculares a esse diametro.
Não sei nem como começar!
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por young_jedi » Qua Jan 09, 2013 20:47
por young_jedi » Qua Jan 09, 2013 20:47
se eu entendi bem a figura é esta

- cone.png (1.79 KiB) Exibido 1283 vezes
com isso temos que traçando seções transversais paralelas a base do cone teremos circunferencias de raio x e pela simetria dos triangulos isocele elas estarão a uma distancia tambe x do vertice do cone
sendo assim a area de cada circunferencia sera
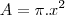
então o volume sera


integrando
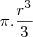
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Volume por seções paralelas
por iarapassos » Seg Jan 07, 2013 12:38
- 0 Respostas
- 988 Exibições
- Última mensagem por iarapassos

Seg Jan 07, 2013 12:38
Cálculo: Limites, Derivadas e Integrais
-
- Volume do Solido
por leha » Qui Dez 10, 2009 10:22
- 3 Respostas
- 3382 Exibições
- Última mensagem por leha

Seg Dez 14, 2009 13:44
Cálculo: Limites, Derivadas e Integrais
-
- Volume de sólido
 por Manoella » Seg Fev 21, 2011 23:41
por Manoella » Seg Fev 21, 2011 23:41
- 1 Respostas
- 2464 Exibições
- Última mensagem por LuizAquino

Ter Fev 22, 2011 11:38
Cálculo: Limites, Derivadas e Integrais
-
- volume de um sólido
 por Andreza » Seg Nov 14, 2011 14:26
por Andreza » Seg Nov 14, 2011 14:26
- 7 Respostas
- 8537 Exibições
- Última mensagem por Andreza

Sex Nov 25, 2011 10:05
Geometria Espacial
-
- volume de um sólido
por Priscila_moraes » Dom Dez 04, 2011 18:55
- 2 Respostas
- 2723 Exibições
- Última mensagem por LuizAquino

Dom Dez 04, 2011 19:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.