 por matmatco » Dom Dez 16, 2012 09:15
por matmatco » Dom Dez 16, 2012 09:15
não estou conseguindo sair dessa raiz ja substitui x= u³ mas minha resposta não bate com a do livro, qual é o meu erro?
![\lim_{x\to3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3} \lim_{x\to3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}](/latexrender/pictures/997ab4ba073e875cf40ba3c42e7f9f12.png)
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por fraol » Dom Dez 16, 2012 10:06
por fraol » Dom Dez 16, 2012 10:06
Bom dia,
Você já tentou multiplicar tanto o numerador quanto o denominador por
![(\sqrt[3]{x}-\sqrt[3]{x}) (\sqrt[3]{x}-\sqrt[3]{x})](/latexrender/pictures/2690ff8091b8e64ccd743847b28b4d7b.png)
, então desenvolver o numerador, o que encontra?
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Dom Dez 16, 2012 10:58
por MarceloFantini » Dom Dez 16, 2012 10:58
Fraol, sua sugestão não resolve. Multiplique e divida por

. Então
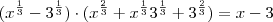
, que poderá ser simplificado com o denominador.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Dom Dez 16, 2012 12:35
por fraol » Dom Dez 16, 2012 12:35
Olá
MarceloFantinifraol escreveu:Bom dia,
Você já tentou multiplicar tanto o numerador quanto o denominador por
![(\sqrt[3]{x}-\sqrt[3]{x}) (\sqrt[3]{x}-\sqrt[3]{x})](/latexrender/pictures/2690ff8091b8e64ccd743847b28b4d7b.png)
, então desenvolver o numerador, o que encontra?
.
Quando escrevi isso tentava mostrar que o numerador é zero, para qualquer x, o que é obvio e nem precisava desse algebrismo pois
![(\sqrt[3]{x}-\sqrt[3]{x}) = 0 (\sqrt[3]{x}-\sqrt[3]{x}) = 0](/latexrender/pictures/e5a2707d09d3ac152e2baa2e50644f87.png)
sempre, certo?
Se assim o for, esse limite é 0, concorda?
Por outro lado, a manipulação algébrica que você propôs é válida, e nesse caso o limite não é zero, se não errei as contas.
Qual é a sua conjectura a respeito?
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Dom Dez 16, 2012 16:03
por MarceloFantini » Dom Dez 16, 2012 16:03
Começa que você não pode fazer isso pois você estaria dividindo por zero, então sua sugestão deixa de ser válida a partir disso. Sim, o limite é diferente de zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Dom Dez 16, 2012 16:14
por fraol » Dom Dez 16, 2012 16:14
Sim, não podemos dividir por zero. Mas eu ainda não substitui o x por 3. Apenas estou simplificando o numerador para depois partir para o cálculo do limite.
Note que na função original o domínio é R\{3}. Então existe f(1), f(2), f(4) e infinitos outros e todos eles são iguais a zero. Então afirmo que o limite é 0.
Por exemplo, qual é o valor de f(1) nessa fatoração/simplificação que você sugere?
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Dom Dez 16, 2012 17:32
por MarceloFantini » Dom Dez 16, 2012 17:32
A função que propos,
![\sqrt[3]{x} - \sqrt[3]{x} \sqrt[3]{x} - \sqrt[3]{x}](/latexrender/pictures/35e90c0586a42dcf8b094cde568d769c.png)
é a função identicamente nula, pois ela é zero em todos os pontos. Novamente, você está essencialmente multiplicando tudo por zero e dizendo que o resultado é zero. Ora, por esse raciocínio então o limite

é zero, pois multiplicando e dividindo

teremos que o limite é zero.
Vou tornar a pergunta para você: por que multiplicar por isto? Qual é o seu argumento para multiplicar tudo por zero, alterar completamente o limite e portanto afirmar que é zero?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por fraol » Dom Dez 16, 2012 17:46
por fraol » Dom Dez 16, 2012 17:46
Eu não multipliquei por 0, nem propus uma nova função. Eu, apenas, estou sugerindo que simplifiquemos o numerador e depois vamos ao cálculo do limite, como normalmente fazemos. Você chegou a verificar os valores de f(x) para x diferente de 3 na função original proposta pelo nosso colega?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por fraol » Dom Dez 16, 2012 17:52
por fraol » Dom Dez 16, 2012 17:52
Opa, desculpe, reli agora o enunciado e vi que trata-se de
![\sqrt[3]{x} - \sqrt[3]{3} \sqrt[3]{x} - \sqrt[3]{3}](/latexrender/pictures/0788f790cf907f8c7b649e43062460f1.png)
no numerador.
Logo ignorem minhas considerações anteriores. Vou ao oculista o mais breve possível ...
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6641 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7252 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4432 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\to3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3} \lim_{x\to3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}](/latexrender/pictures/997ab4ba073e875cf40ba3c42e7f9f12.png)


![(\sqrt[3]{x}-\sqrt[3]{x}) (\sqrt[3]{x}-\sqrt[3]{x})](/latexrender/pictures/2690ff8091b8e64ccd743847b28b4d7b.png) , então desenvolver o numerador, o que encontra?
, então desenvolver o numerador, o que encontra?
 . Então
. Então 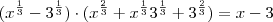 , que poderá ser simplificado com o denominador.
, que poderá ser simplificado com o denominador.

, então desenvolver o numerador, o que encontra?
![(\sqrt[3]{x}-\sqrt[3]{x}) = 0 (\sqrt[3]{x}-\sqrt[3]{x}) = 0](/latexrender/pictures/e5a2707d09d3ac152e2baa2e50644f87.png) sempre, certo?
sempre, certo?



![\sqrt[3]{x} - \sqrt[3]{x} \sqrt[3]{x} - \sqrt[3]{x}](/latexrender/pictures/35e90c0586a42dcf8b094cde568d769c.png) é a função identicamente nula, pois ela é zero em todos os pontos. Novamente, você está essencialmente multiplicando tudo por zero e dizendo que o resultado é zero. Ora, por esse raciocínio então o limite
é a função identicamente nula, pois ela é zero em todos os pontos. Novamente, você está essencialmente multiplicando tudo por zero e dizendo que o resultado é zero. Ora, por esse raciocínio então o limite  é zero, pois multiplicando e dividindo
é zero, pois multiplicando e dividindo  teremos que o limite é zero.
teremos que o limite é zero.


![\sqrt[3]{x} - \sqrt[3]{3} \sqrt[3]{x} - \sqrt[3]{3}](/latexrender/pictures/0788f790cf907f8c7b649e43062460f1.png) no numerador.
no numerador.