 por vinicastro » Sáb Dez 15, 2012 22:42
por vinicastro » Sáb Dez 15, 2012 22:42
calcule a derivada de ordem 33 da função f(x)=sen(x)+e^x/2.
eu comecei mais fique com duvidas f'=cos(x)+e^x/2*1/2 nem sei se ta certo.
-
vinicastro
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Dez 15, 2012 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
 por e8group » Sáb Dez 15, 2012 23:04
por e8group » Sáb Dez 15, 2012 23:04
Boa noite , qual das três funções a seguir corresponde com a do enunciado .
i)
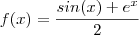
ii)
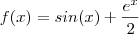
iii)

Qual das três ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por vinicastro » Dom Dez 16, 2012 09:58
por vinicastro » Dom Dez 16, 2012 09:58
é a terceira.
-
vinicastro
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Dez 15, 2012 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
 por vinicastro » Dom Dez 16, 2012 10:06
por vinicastro » Dom Dez 16, 2012 10:06

É ESSA AQUI, ESTOU APRENDENDO USAR AS FERRAMENTAS AINDA.
-
vinicastro
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Dez 15, 2012 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
 por e8group » Dom Dez 16, 2012 13:57
por e8group » Dom Dez 16, 2012 13:57
OK !
Note que ,

e
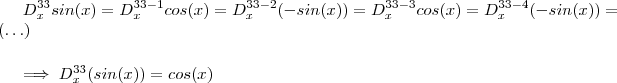
.
Basta observar o comportamento acima de cada derivação ,assim chega-se na resposta acima , Logo
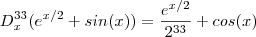
.
Qual quer dúvida só comentar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por vinicastro » Dom Dez 16, 2012 15:57
por vinicastro » Dom Dez 16, 2012 15:57
poxa muito obrigado.
mas o sinal da explicação ficou trocado
y=sen(x)
y'=cos(x)
y''=-sen(x)
y'''=-cos(x)
y^4=sen(x)
-
vinicastro
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Dez 15, 2012 22:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- derivadas como fazer essa questão
por eulercx » Qua Dez 16, 2015 23:48
- 2 Respostas
- 5178 Exibições
- Última mensagem por eulercx

Qui Jan 14, 2016 10:22
Cálculo: Limites, Derivadas e Integrais
-
- Não consigo calcular essa derivada!!!
por Catalao » Qua Mai 09, 2012 19:51
- 3 Respostas
- 2357 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 14:55
Cálculo: Limites, Derivadas e Integrais
-
- Como integrar essa derivada: ?2/(3x²+2)dx
por Therodrigou » Ter Set 18, 2018 03:08
- 3 Respostas
- 7962 Exibições
- Última mensagem por Gebe

Ter Set 18, 2018 15:36
Cálculo: Limites, Derivadas e Integrais
-
- Preciso de ajuda com essa derivada [resolvido]
por schmitt » Sáb Abr 09, 2011 15:52
- 2 Respostas
- 2049 Exibições
- Última mensagem por schmitt

Sáb Abr 09, 2011 17:27
Cálculo: Limites, Derivadas e Integrais
-
- Não consigo resolver essa questão com derivada
por Cristiano Tavares » Sáb Jun 18, 2011 12:18
- 2 Respostas
- 1827 Exibições
- Última mensagem por Cristiano Tavares

Sáb Jun 18, 2011 15:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



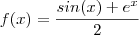
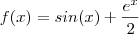






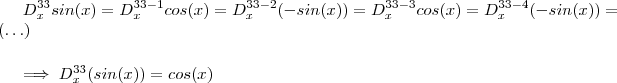 .
.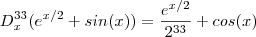 .
.


 .
.



