 por ghf » Sáb Nov 03, 2012 17:30
por ghf » Sáb Nov 03, 2012 17:30
Olá!
Tenho que encontrar os intervalos onde a função abaixo é crescente e decrescente

Derivando ela tenho:
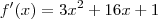
As raízes da função derivada são:
x1 =
![\frac{1}{3}(-8 - \sqrt[]{61}) \frac{1}{3}(-8 - \sqrt[]{61})](/latexrender/pictures/36eaa3ce0de0264454c71b0d1c6d24ab.png)
x2 =
![\frac{1}{3}(-8 + \sqrt[]{61}) \frac{1}{3}(-8 + \sqrt[]{61})](/latexrender/pictures/8e75623efbc783f85a9dd1a0f0a7aad7.png)
E aí que eu me perco... Na hora de analisar a função e as raízes.
Em funções do primeiro grau eu consigo, mas essa do segundo grau não estou conseguindo desenvolver!
Alguma ajuda de qual próximo passo eu devo seguir?
Obrigado!
-
ghf
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 02, 2012 22:26
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Sáb Nov 03, 2012 18:22
por e8group » Sáb Nov 03, 2012 18:22
Basta atribuir valores a e esquerda e a direita das raízes e denotar o comportamento . Vamos lá ,

e
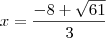
.
Vamos pegar valores testes :
Por exemplo ,
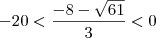
e
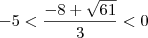
.
i)


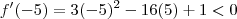
Com estas conclusões e lembrando que f é contínua . teremos que :

é crescente :

Decrescente :
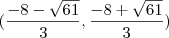
.
Editado . Escrevi algumas coisas erroneamente .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Nov 04, 2012 13:56
por e8group » Dom Nov 04, 2012 13:56
Boa tarde , por favor olhe este link abaixo (acho que ficou mais claro agora ):
http://en.wikipedia.org/wiki/Derivative ... derivative Observe bem , veja que a taxa de variação (Derivada de primeira ordem de f), orá fica positiva , negativa e nula , de acordo com exemplo acima . Sendo assim , quando você atribui valores testes a
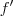
, genericamente
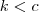
e

tal que
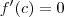
, podemos estudar o comportamento da função . Vamos supor que tenhamos duas situações .
1)

e

Nesta situação , perceba que pegamos valores testes menores e maiores que

, lembrando que

é o valor para o qual a derivada de f é nula . Assim , generalizando , se

é contínua em
![[a,b ] [a,b ]](/latexrender/pictures/2b52c95974d7d69daa6ffc2a7133cd1d.png)
e
![k,p,c \in [a,b] k,p,c \in [a,b]](/latexrender/pictures/236a7cb054558b7f08363abc88ef3833.png)
. Podemos dizer que

é crescente em ,
![(c,b] (c,b]](/latexrender/pictures/b466764345f65101578c320f03d4bfae.png)
e decrescente em

. Note que nesta situação , a derivada fica negativa para todos valores pertencentes

e positiva para todos valores em
![(c,b] (c,b]](/latexrender/pictures/b466764345f65101578c320f03d4bfae.png)
.
A situação 2 é ao contrário da primeira . OBS.: Se tiver com dúvida , recomendo as aulas do Prof. Luis Aquino no canal do youtube .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14802 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Achar a derivada de uma função
por caiofisico » Seg Set 05, 2011 20:18
- 4 Respostas
- 3849 Exibições
- Última mensagem por caiofisico

Ter Set 06, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
-
- ]Derivada de uma função] derivada com raiz
por Leandro_Araujo » Ter Mar 06, 2012 01:11
- 5 Respostas
- 8557 Exibições
- Última mensagem por LuizAquino

Ter Mar 06, 2012 13:40
Cálculo: Limites, Derivadas e Integrais
-
- derivada de uma função
por jmario » Sex Mai 07, 2010 13:51
- 4 Respostas
- 3798 Exibições
- Última mensagem por Elcioschin

Sex Mai 07, 2010 23:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

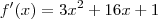
![\frac{1}{3}(-8 - \sqrt[]{61}) \frac{1}{3}(-8 - \sqrt[]{61})](/latexrender/pictures/36eaa3ce0de0264454c71b0d1c6d24ab.png)
![\frac{1}{3}(-8 + \sqrt[]{61}) \frac{1}{3}(-8 + \sqrt[]{61})](/latexrender/pictures/8e75623efbc783f85a9dd1a0f0a7aad7.png)


 e
e 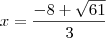 .
. 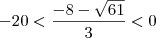 e
e 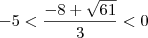 .
.

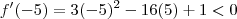
 é crescente :
é crescente : 
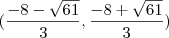 .
.
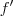 , genericamente
, genericamente 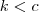 e
e  tal que
tal que 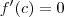 , podemos estudar o comportamento da função . Vamos supor que tenhamos duas situações .
, podemos estudar o comportamento da função . Vamos supor que tenhamos duas situações . e
e 
 , lembrando que
, lembrando que ![[a,b ] [a,b ]](/latexrender/pictures/2b52c95974d7d69daa6ffc2a7133cd1d.png) e
e ![k,p,c \in [a,b] k,p,c \in [a,b]](/latexrender/pictures/236a7cb054558b7f08363abc88ef3833.png) . Podemos dizer que
. Podemos dizer que ![(c,b] (c,b]](/latexrender/pictures/b466764345f65101578c320f03d4bfae.png) e decrescente em
e decrescente em  . Note que nesta situação , a derivada fica negativa para todos valores pertencentes
. Note que nesta situação , a derivada fica negativa para todos valores pertencentes 

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.