 por CarolMarques » Sex Nov 02, 2012 13:18
por CarolMarques » Sex Nov 02, 2012 13:18
![\lim_{\rightarrow -1} \left[\frac{1}{1-x} - \frac{2}{1-{x}^{2}}\right] \lim_{\rightarrow -1} \left[\frac{1}{1-x} - \frac{2}{1-{x}^{2}}\right]](/latexrender/pictures/340e89bb9aeb25a8ba08d9470572c82a.png)
Fazendo o cálculo desse limite eu acho

, mas o gabarito que eu tenho esta - 1/2.Quando eu coloquei essa expressão em uma calculadora de limite eu achei como resposta

.
Eu resolvo da seguinte forma:
Aplico a propriedade dos limites separando os limites para depois subtrair os resultados
Assim no final fica
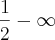
que é igual a

.
Tem algum erro no meu raciocinio?
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por e8group » Sex Nov 02, 2012 13:46
por e8group » Sex Nov 02, 2012 13:46
Sua resolução estar correta
veja aqui . Agora se naverdade , x tende a 1 pela esquerda

, o resultado é como consta no gabarito , veja esta opção
aqui ! .
Como dica , recomendo este site que utilizei acima para vc checkar o resultado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvida no Limte
por CarolMarques » Sex Nov 02, 2012 15:58
- 1 Respostas
- 1043 Exibições
- Última mensagem por MarceloFantini

Sex Nov 02, 2012 16:21
Cálculo: Limites, Derivadas e Integrais
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11055 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida PA
por Cleyson007 » Dom Jun 01, 2008 01:01
- 2 Respostas
- 10764 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Progressões
-
- Dúvida
por miguelbaptista » Sex Jan 09, 2009 03:29
- 8 Respostas
- 12528 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:13
Logaritmos
-
- dúvida
por gdarius » Dom Ago 16, 2009 00:09
- 1 Respostas
- 3155 Exibições
- Última mensagem por Felipe Schucman

Dom Ago 16, 2009 02:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{\rightarrow -1} \left[\frac{1}{1-x} - \frac{2}{1-{x}^{2}}\right] \lim_{\rightarrow -1} \left[\frac{1}{1-x} - \frac{2}{1-{x}^{2}}\right]](/latexrender/pictures/340e89bb9aeb25a8ba08d9470572c82a.png)
 , mas o gabarito que eu tenho esta - 1/2.Quando eu coloquei essa expressão em uma calculadora de limite eu achei como resposta
, mas o gabarito que eu tenho esta - 1/2.Quando eu coloquei essa expressão em uma calculadora de limite eu achei como resposta  .
.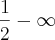 que é igual a
que é igual a  .
.

 , o resultado é como consta no gabarito , veja esta opção
, o resultado é como consta no gabarito , veja esta opção 