é dado essa integral:
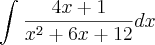
Ai como:
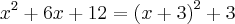
Então:
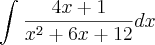 =
= 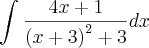
Ai calculando:
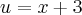 e
e 
Então:
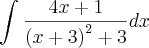 =
=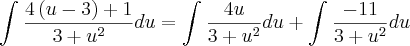
Mas agora estou em duvida pois integrando da um pouco diferente da resposta:
A resposta é:
![2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c 2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c](/latexrender/pictures/436e38928dc02ff158279cd65b749d51.png)
Me ajudem nessa questão por favor..Obrigado!

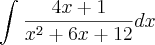
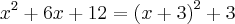
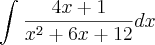 =
= 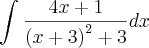
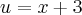 e
e 
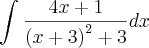 =
=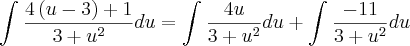
![2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c 2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c](/latexrender/pictures/436e38928dc02ff158279cd65b749d51.png)

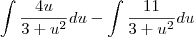
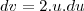
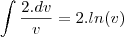
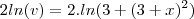

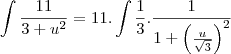
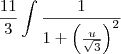
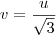
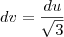
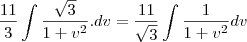
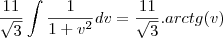
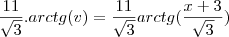
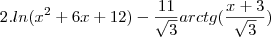


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: