Tenho que derivar esta função
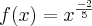 .
.Derivando de forma direta, não encontro problema algum...

E resolvendo tudo no final encontro o resultado de:

Agora eu não consigo entender ( e vejo que estou falhando com conceitos de matemática básica) se eu partir para resolver, antes de derivar, "ajeitando" a expressão.
Por exemplo:
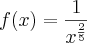
Gostaria que me descrevessem o desenrolar desta solução até a resposta final, pois tentei vários métodos e não chego ao final.



 ,
,


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)