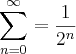 com erro menor que 2%
com erro menor que 2%Resolução
 + .........
+ .........n = 0 S = 1 Erro=
n=1 S = 1,5 Erro=
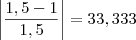 %
%n=2 S=1,75 Erro=
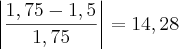 %
%n=3 S=1,875 Erro=
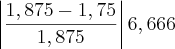 %
%n=4 S=1,9375 Erro=
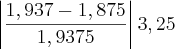 %
%n=5 S=1,9687 Erro=
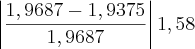 %
% O que eu não entendi o porque quando vamos calcular o erro pegamos no caso de n =2, o valor de arredondamento como 1,5 e não valor posterior de 1,875
2-Um aluno resolveu somar a seqüência
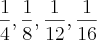 .... até o 5º termo. O outro aluno resolveu somar até o 6º termo . Calcule os erros absolutos e relativos entre os resultados dos dois alunos, tomados com 4 casas decimais
.... até o 5º termo. O outro aluno resolveu somar até o 6º termo . Calcule os erros absolutos e relativos entre os resultados dos dois alunos, tomados com 4 casas decimaisresolução
5º termo = 0,5708
6º termo = 0,6125
Erro absoluto=
 =0,0417
=0,0417Erro relativo=
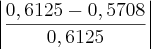 = 6,81%
= 6,81%Eu não entendi porque o 5º termo foi usado como o arredondamento
Valeu
Danilo



 .
.
 :
: