 por filipeferminiano » Qui Ago 26, 2010 16:42
por filipeferminiano » Qui Ago 26, 2010 16:42
Boa tarde, estou iniciando meu estudo sobre limites e ainda não entendi como se acha o valor mínimo de

.
Por exemplo:
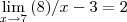
Eu não entendi muito bem a lógica do meu livro, quando ele diz que:

e isso seria equivalente a
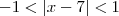
Alguém saberia me explicar como é a lógica desse exercício?
-
filipeferminiano
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Ago 26, 2010 16:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Marketing
- Andamento: cursando
 por MarceloFantini » Qui Ago 26, 2010 17:42
por MarceloFantini » Qui Ago 26, 2010 17:42
É esse o limite:
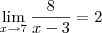
? Se sim, é fácil,

pertence ao domínio e o limite existe:
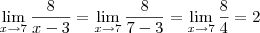
.
Com relação ao módulo, não é difícil. Lembre-se que módulo é a distância até a origem. Então, por exemplo, se
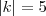
. então o número

ou é 5 ou é -5. Se for uma desigualdade, isso quer dizer um conjunto de números que satisfaz a condição. Exemplo:
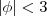
quer dizer todos os números cuja distância é menor que 3, sejam positivos ou negativos (distância são sempre números positivos pois não existe distância negativa. Assim,

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por filipeferminiano » Sex Ago 27, 2010 00:30
por filipeferminiano » Sex Ago 27, 2010 00:30
Muito obrigado, essa parte eu entendi. Mas, o exercício pede para provar que o limite dessa função é 2 quando x tende a 7, mostrando que para qualquer

haja um
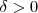
.
Então, pulando algumas partes da resolução ele chega em

, então, certamente
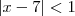
, eu gostaria de saber de onde veio esse 1,
-
filipeferminiano
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Ago 26, 2010 16:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Marketing
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ACHAR ANGULO
por karenblond » Qua Abr 07, 2010 14:58
- 1 Respostas
- 1389 Exibições
- Última mensagem por Molina

Qua Abr 07, 2010 20:11
Geometria Plana
-
- Achar valor de b
por Carolziiinhaaah » Qui Ago 05, 2010 12:32
- 1 Respostas
- 1350 Exibições
- Última mensagem por MarceloFantini

Qui Ago 05, 2010 13:48
Funções
-
- Achar valor de f(-3)
por Carolziiinhaaah » Qui Ago 12, 2010 11:29
- 5 Respostas
- 12888 Exibições
- Última mensagem por Carolziiinhaaah

Sex Ago 13, 2010 17:08
Funções
-
- Achar a função
por will » Qua Abr 06, 2011 20:52
- 0 Respostas
- 1196 Exibições
- Última mensagem por will

Qua Abr 06, 2011 20:52
Funções
-
- Achar derivada
por Kathleen » Dom Jun 26, 2011 19:20
- 5 Respostas
- 2904 Exibições
- Última mensagem por Neperiano

Dom Jun 26, 2011 21:59
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.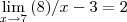
 e isso seria equivalente a
e isso seria equivalente a 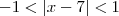

 .
.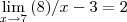
 e isso seria equivalente a
e isso seria equivalente a 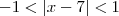

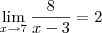 ? Se sim, é fácil,
? Se sim, é fácil,  pertence ao domínio e o limite existe:
pertence ao domínio e o limite existe: 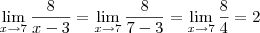 .
.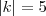 . então o número
. então o número  ou é 5 ou é -5. Se for uma desigualdade, isso quer dizer um conjunto de números que satisfaz a condição. Exemplo:
ou é 5 ou é -5. Se for uma desigualdade, isso quer dizer um conjunto de números que satisfaz a condição. Exemplo: 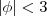 quer dizer todos os números cuja distância é menor que 3, sejam positivos ou negativos (distância são sempre números positivos pois não existe distância negativa. Assim,
quer dizer todos os números cuja distância é menor que 3, sejam positivos ou negativos (distância são sempre números positivos pois não existe distância negativa. Assim,  .
.

 haja um
haja um 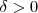 .
. , então, certamente
, então, certamente 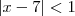 , eu gostaria de saber de onde veio esse 1,
, eu gostaria de saber de onde veio esse 1,
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
