 por LFurriel » Dom Jul 25, 2010 22:41
por LFurriel » Dom Jul 25, 2010 22:41
Olá, realizei uma prova da usp hoje, e após conferir o gabarito fiquei com uma dúvida.
http://www.fuvest.br/tran2011/provas/tran2011.exa.pdf ..
a questao 43, da pagina 8, me deixou intrigada.
Pois para mim, a resposta seria a alternativa d, contraria ao que diz no gabarito, que aponta a B como correta.
Gostaria que alguem me explicasse o porque. Obrigada!
-
LFurriel
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Jul 23, 2010 23:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LFurriel » Seg Jul 26, 2010 00:07
por LFurriel » Seg Jul 26, 2010 00:07
Ola, só nao entendi pq o primeiro limite vale 0 e nao 2.
Pois nao seria 2 multiplicando um limite notavel de sen(x)/x qe vale 1?
por isso pra mim a resposta seria 5/2, pois seria esse 2 somado a 1/2 da segunda expressão.
Obrigada!
-
LFurriel
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Jul 23, 2010 23:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Lucio Carvalho » Seg Jul 26, 2010 00:18
por Lucio Carvalho » Seg Jul 26, 2010 00:18
Olá LFurrier,
Atenção! No primeiro limite não temos x a tender para zero.
No segundo, apesar de termos x a tender para mais infinito, no numerador está sen(1/x) e no denominador (1/x). É o mesmo que termos x a tender para zero e, no numerador existir sen x e no denominador x.
Espero que tenhas compreendido.
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por LFurriel » Seg Jul 26, 2010 00:31
por LFurriel » Seg Jul 26, 2010 00:31
Desculpa a insistência, mas ainda nao compreendi ..
pois para utilizei o seguinte raciocinio, usando 1/x =v, quando "x" tender para o infinito "v" vai tender para zero, e isso vale para os dois.
como o somente o segundo é utilizado do limite notavel?
Usando entao x = 1/v. Fazendo a substituição e fazendo a nova variável tender para zero vem:
limite x --> +inf de 2(senx)/x + (x/2)sen(1/x) =
limite x --> 0 de 2[sen(1/v)/(1/v)] + (1/2v)sen(v) =
limite x --> 0 de 2[sen(1/v)/(1/v)] + (1/2)(senv)/v =
limite x --> 0 de 2[1] + (1/2)(1) =
2+1/2 = 5/2
Chegando na letra "d".
Queria entender!
Obrigada pela paciencia!
-
LFurriel
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Jul 23, 2010 23:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Seg Jul 26, 2010 15:28
por MarceloFantini » Seg Jul 26, 2010 15:28
No limite fundamental da função seno, o denominador tem que sempre tender a zero, qualquer que seja ele.

, o denominador tende a zero, portanto caracteriza o limite fundamental. Vou fazer com a mudança de variável que você fez:

tal que
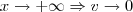
:

Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Erro na prova?
por kandara » Ter Jun 17, 2014 01:18
- 0 Respostas
- 1925 Exibições
- Última mensagem por kandara

Ter Jun 17, 2014 01:18
Geometria Espacial
-
- [Limites] Limites no "infinito " prova a existência ......
por e8group » Dom Jun 17, 2012 14:37
- 2 Respostas
- 2749 Exibições
- Última mensagem por e8group

Ter Jun 19, 2012 11:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Prova de limites
por IlgssonBraga » Sáb Fev 08, 2014 17:32
- 5 Respostas
- 4791 Exibições
- Última mensagem por e8group

Qui Fev 13, 2014 19:45
Cálculo: Limites, Derivadas e Integrais
-
- [teoria de limites] dúvida numa questão de prova
por Fabio Wanderley » Sex Abr 13, 2012 23:38
- 2 Respostas
- 1944 Exibições
- Última mensagem por Fabio Wanderley

Sáb Abr 14, 2012 00:43
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] duas variáveis. Prova através da definição formal
por marcosmuscul » Sáb Jan 25, 2014 17:59
- 2 Respostas
- 6101 Exibições
- Última mensagem por marcosmuscul

Ter Fev 04, 2014 10:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , o denominador tende a zero, portanto caracteriza o limite fundamental. Vou fazer com a mudança de variável que você fez:
, o denominador tende a zero, portanto caracteriza o limite fundamental. Vou fazer com a mudança de variável que você fez:  tal que
tal que 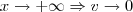 :
: 


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.